9 - 字符串匹配

学学字符串的匹配算法，例如单模式串匹配的KMP算法和Sunday算法；多模式串TODO。

单模式串匹配

KMP算法

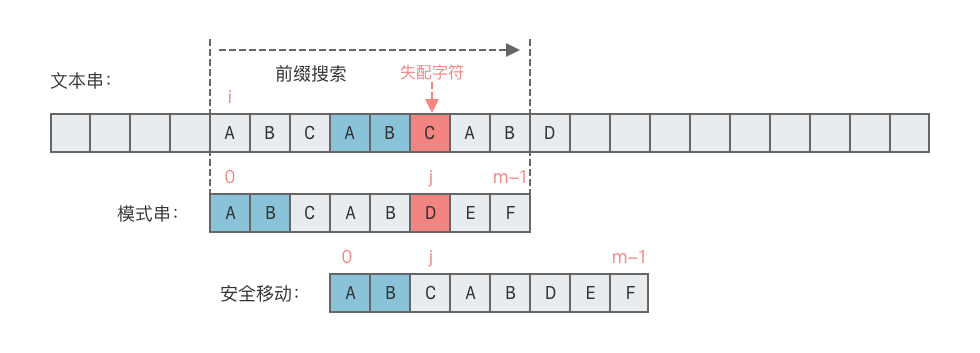
KMP算法对模式串p进行了预处理，计算出next数组。在每次失配发生时，不回退文本串里的指针i，而是根据next数组中模式串失配位置j的前一个位置的值next[j - 1]决定模式串可以向右移动的次数。如下图所示：

可以发现在前j-1的模式子串ABCAB中拥有相同前后缀AB，那么失配后下次的比较就能跳过对前缀AB的比较，从而节省一定的时间。因此next[j]的含义就是：记录下标 j 之前（包括j）的模式串 p 中，最长相等前后缀的长度。

可以通过递推的方式构造next数组：

1. 将模式串p拆分成left和right两部分。left表示前缀串开始所在的位置，right表示后缀串开始所在的位置。起始left = 0, right = 1。
2. 比较p[left]是否和p[right]相等：
   1. p[left] == p[right]：前后缀相同，让left += 1，此时left既是前缀下一次比较的位置，又是当前最长相同前后缀的长度。
   2. p[left] != p[right]：前后缀不相同，让后缀开始位置k不动，前缀left不断回退next[left - 1]，直至p[left] == p[right]。
3. 记录下标right之前的模式串p中，最长相同前后缀的长度为left。即next[right] = left。

代码如下：

vector<int> GenerateNext(const std::string& pattern)
{
    int n = pattern.length();
    vector<int> next(n);
    
    int left = 0;
    for (int right = 1; right < n; ++right)
    {
        // 匹配不成功就让left一直回退next[left - 1]
        while (left > 0 && pattern[left] != pattern[right])
        {
            left = next[left - 1];
        }
        
        // 匹配成功就让left+1
        if (pattern[left] == pattern[right])
        {
            left++;
        }
        
        // 更新next[right]
        next[right] = left;
    }
    
    return next;
}

有了next数组后，便能进行比较了，KMP算法的步骤如下：

1. 求next数组；
2. 用i, j两个指针进行比较，i遍历文本串，j遍历模式串；
3. 判断t[i]和p[j]是否相同：
   1. 不相同，一直回退模式串j = next[j - 1]，直至j == 0或者前缀比较成功。
   2. 相同，如果是部分匹配成功，就让j和i继续匹配下去；如果是全部匹配成功，就返回匹配成功的开始位置i - j + 1。
4. 如果从未完全匹配成功，说明匹配失败。

代码如下：

int kmp(const string& target, const string& pattern)
{
    vector<int> next = GenerateNext(pattern);
    for (int i = 0, j = 0; i < target.length() ++i)
    {
        // 匹配不成功, 就一直回退
        while (j > 0 && target[i] != pattern[j])
        {
            j = next[j - 1];
        }
        // 部分匹配成功, 继续
        if (target[i] == pattern[j])
        {
            j++;
        }
        // 完全匹配成功, 返回匹配开始位置
        if (j == pattern.length())
        {
            return i - j + 1;
        }
    }
    
    // 匹配失败
    return -1;
}

KMP算法的时间复杂度是O(m + n)，时间花费在构造next数组和遍历文本串上了。

Sunday算法

TODO

多模式串匹配

TODO

参考资料

• 算法通关手册（LeetCode） | 算法通关手册（LeetCode） (itcharge.cn)