04 - 蒙特卡洛路径追踪

在这篇文章中，要使用蒙特卡洛路径追踪来完成“全局光照”这一目标，解决渲染方程的计算问题。

蒙特卡洛积分

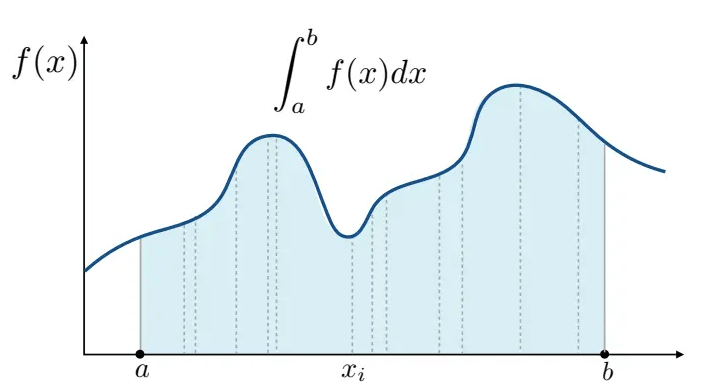
给定一个函数，求解它从a到b的定积分，但他解析式写不出来，这时候就要用蒙特卡洛积分(Monte Carlo Integration)去近似求解它的值。

原理

蒙特卡洛积分的原理就是对函数值进行多次采样求均值作为积分值的近似。

例如对上图函数进行采样，假设采到了$x_i$，那么就计算长ab，宽$f(x_i)$的长方形的面积。进行多次采样，得到多个长方形的面积，然后对他们求均值，就能近似得到该定积分的值。

定义

希望求出函数$f(x)$在$[a,b]$上的定积分，选定一个采样分布（PDF）$p(x)$，使用该分布对$f(x)$进行多次采样，最后估计出来的值就是$F_N$。

这里默认使用 均匀随机分布(Uniform random variable)，代入$F_N$得到：

经典光追存在的问题

经典的Whitted-Style光线追踪做了如下事情：

• 进行光滑面的折射、反射
• 在漫反射面上取消光线弹射

但这样并不怎么合理，不符合一些物理规则。

例如下图的两个茶壶，左边这个Specular材质的让光线做镜面反射，经典光追可以做到；但右边Glossy材质那种金属般光泽的反射，经典光追做不来：

再例如下图的两个盒子，其实光线射到漫反射面上，也会让光线反射，只是反射到不同的方向上，但经典光追却不考虑这一点。以Path Tracing为例，经典光追就是左图直接光照的效果；右图全局光照让光线漫反射面上反弹，有着color bleeding效果（红墙的光反射到长方体上，那个面也红了）：

因此，经典光追是错误的，要按着渲染方程来。

路径追踪(Path Tracing)

路径追踪可以渲染出照片级真实感的图片：

蒙特卡洛求积分

渲染方程如下：

$$\nonumber L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n·\omega_i)\mathrm{d}\omega_i$$

观察这个方程，可以发现：

• 要求解对整个半球的积分
• 需要递归求解的光照未知项

这些问题影响了渲染方程的计算。

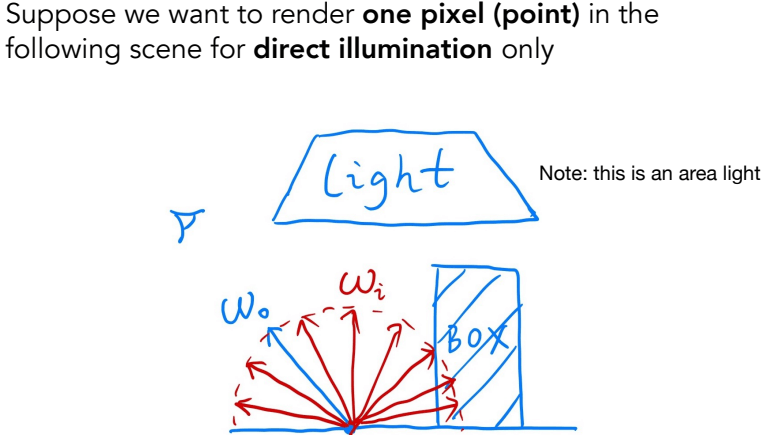
首先解决求积分的问题，该半球积分可以用蒙特卡洛方法来做。以下图为例，仅考虑直接光照，且假设入射和反射光方向都朝外。

在本例中，$f(x)=\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n·\omega_i)\mathrm{d}\omega_i$，PDF $p(\omega_i)=1/2\pi$，因为半球面积是$2\pi$。

带入蒙特卡洛积分的式子里，那么半球积分的值约等于

$$\nonumber \frac{1}{N}\sum^N_{i=1}\frac{L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n·\omega_i)}{p(\omega_i)}$$

伪代码如下：

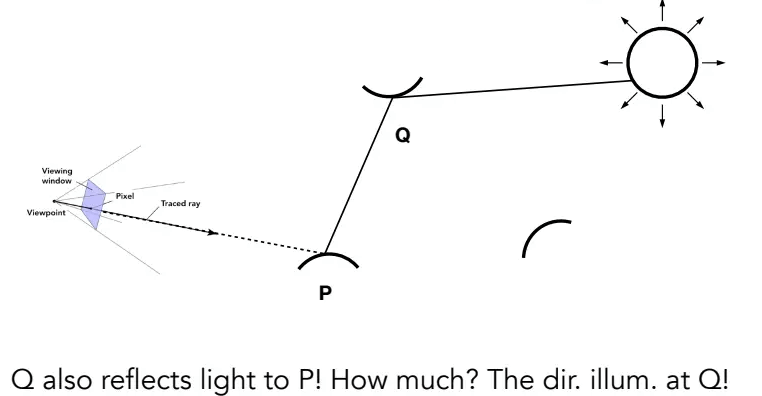
接下来引入间接光照：

P点接收到Q反射的光源，也能将此看成“直接光”，从而递归地进行计算。

问题分析与解决

现在路径追踪的主体部分已完成，就剩下一些问题的分析和优化了。

计算量太大

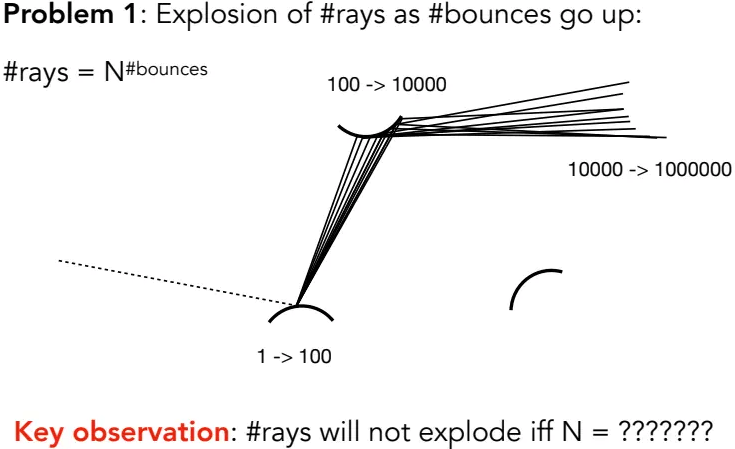
但是这样做直接体现出来的问题就是 计算量太大：

假设每次采样$N=100$条，那么打出的光线数就是$100^\text{反弹次数}$条，发生指数爆炸。因此为了避免指数爆炸，得让$N=1$，这就是路径追踪。

Ps：当$N\neq1$时，被称为分布式光线追踪，是历史遗留问题。

路径追踪的伪代码如下：

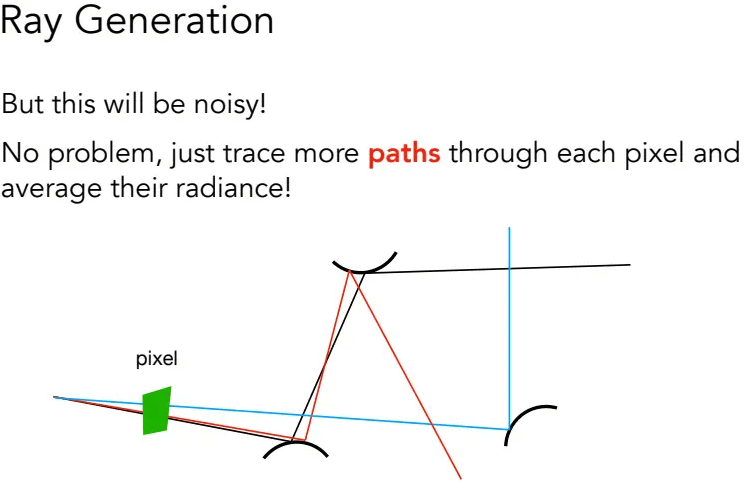
但只采样1次，求出来的积分不准确。只需从被渲染的像素出发，通过在每个像素中遍历寻找更多的路径，将结果求平均值即可：

这种操作叫Ray Generation，它的伪代码如下：

也像是在求一个蒙特卡洛积分。

没有递归出口

观察路径追踪的伪代码，发现它还没有递归出口。如果以光线反弹次数为标准，不符合物理规律。可以使用 俄罗斯轮盘赌（Russian Roulette）来解决这个问题。

我们人为设定一个概率$P$，有$P$的概率进行路径追踪，返回$L_o/P$；有$1-P$的概率不进行路径追踪，返回0。我们再使用离散型随机变量的期望获得路径追踪的着色结果$L_o$:

$$\nonumber E=P(L_o/P)+(1-P)\times0=L_o$$

十分天才的设计，既提供了递归出口又返回正确的$L_o$。改进后的伪代码如下：

经过优化后，我们已经得到正确的路径追踪算法了：

可以发现，效果是正确的，但在不同采样率（SPP，每像素进行几次路径追踪）的效果还是有差别的。

效率优化

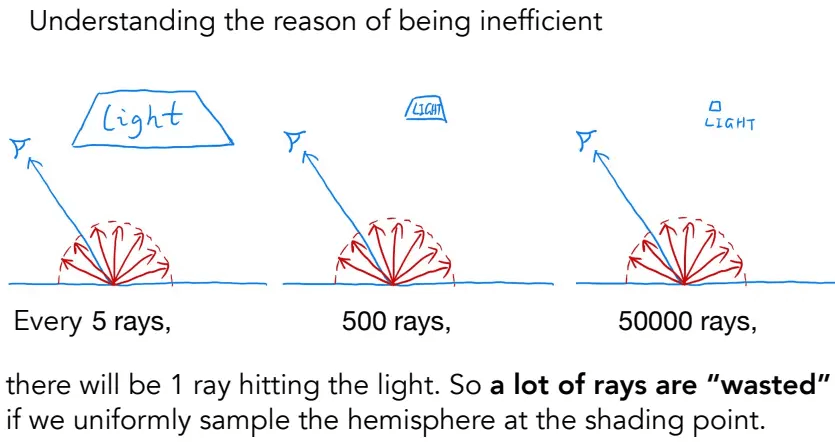
通过均匀采样，朝不同方向射出光线去寻找光源，但光源越小，射出更多的光线才能找到光源，这导致大量的光线被浪费了。

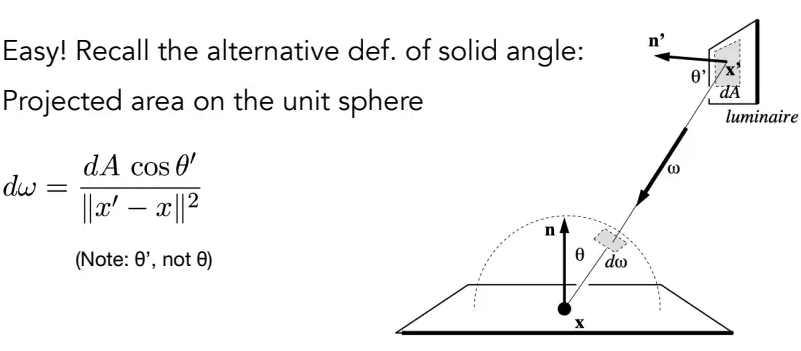
可以改进一下采样方法，直接对光源进行采样，这样没有光线被浪费。令光源面积为A，那么对光源进行均匀采样的$PDF=1/A$。由于之前是对光线采样，对光源方向$d\omega_i$积分，现在变成对光源采样，那就得对光源面积$dA$积分，因此还得对原来的积分进行换元：

如上图所示，根据立体角的定义$\mathrm{d}\omega=\mathrm{d}A/r^2$，可以得到换元的关系式。需要注意的是，这里的$\mathrm{d}A$和图上的不同，需要进行投影变换得到正对球心的才行。

改写后的积分如下：

$$\nonumber \int_{A}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\frac{\mathrm{cos\theta cos\theta'}}{\|x'-x\|^2}\mathrm{d}A$$

也能用蒙特卡罗方法去解这个积分。

综上，光线传播可以分成以下两部分：

1. 光源直接对该点的贡献，是直接光部分，不需要俄罗斯轮盘赌
2. 其他非光源对该点的贡献，是间接光部分，需要俄罗斯轮盘赌

优化后的伪代码如下：

别高兴的太早，如果着色点和光源间存在物体，如何判断它俩间会不会被物体挡住？很简单，只需发出一条测试光线，判断是否与该物体相交即可：

我还要学习的...

传统与现代光追

• 传统光追：Whitted-Style光线追踪
• 现代光追：
  • （单向、双向）路径追踪
  • 光子映射
  • Metropolis光线传输
  • VCM/UPBP ...

未提到的内容

GAMES101课程中，未提到的内容：

• 如何对采样任意一个函数（采样理论）？
• 蒙特卡洛积分，如何选择最优的PDF（重要性采样理论）？
• 随机数的质量好坏？（Low discrepancy 序列）
• 如何将两种采样方法结合起来，使得最后结果看起来更好，如上边半球和光源的采样？（MIS，Multiple Importance Sampling）
• 一个像素的radiance是所有通过它路径贡献的平均值（Pixel Reconstruction Filter）
• 像素的颜色不是算下的radiance（伽马校正，曲线，颜色空间）

参考资料

• GAMES101-现代计算机图形学入门
• 计算机图形学十五：全局光照(蒙特卡洛路径追踪) - 知乎 (zhihu.com)