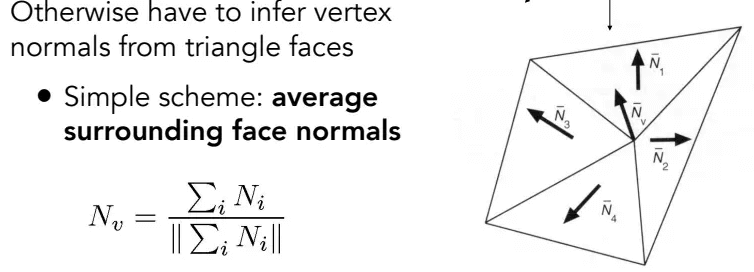02 - 着色频率
着色频率(Shading Frequencies)
着色也分频率：每平面着色，每顶点着色和每像素着色。
着色频率取决于模型精度，模型精度越高（三角形面数多），着色频率可以越低。
平面着色(Flat Shading)
对每个三角形面进行着色，面的法向量可由三角形两条边叉乘得到。
计算快，但效果不怎么好（不光滑）。
顶点着色(Gouraud Shading)
对每个顶点进行着色，三个顶点定义一个三角形，其内部的点通过插值(interpolate)实现着色。
那么顶点的法向量该怎么求？
注意到一个顶点可能会被几个三角形面共用，将所有共享这个点的面的法线向量加起来求均值，最后再标准化就得到了该顶点的法线向量了：
为了更加准确，这个均值也可以是加权的，权为“这几个三角形的面积”，谁面积大，谁贡献就大，权也越大。
像素着色(Phong Shading)
对每个像素进行着色，效果好但计算量大。
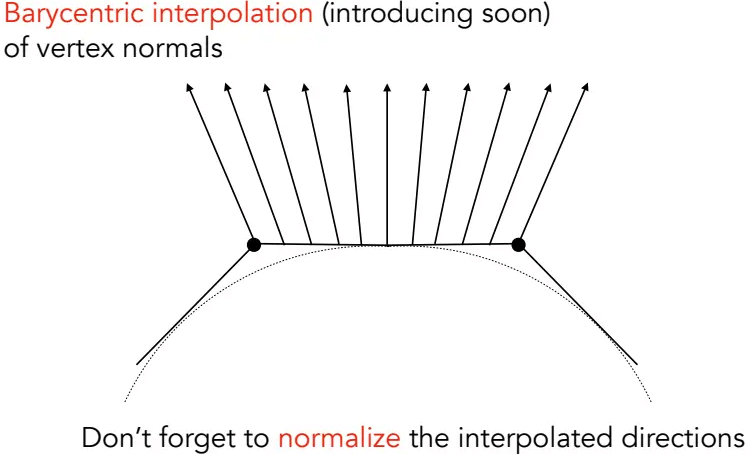
那么每个像素的法向量怎么求？
假设我们知道了每个顶点的法线，那么三角形内部平滑过渡的法线可以通过插值得到。
