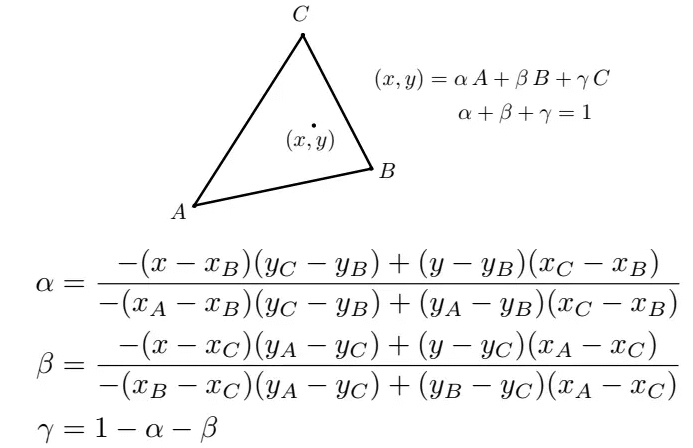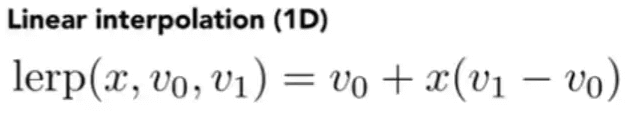跳到主要内容

05 - 插值

重心坐标系(Barycentric coordinates)​

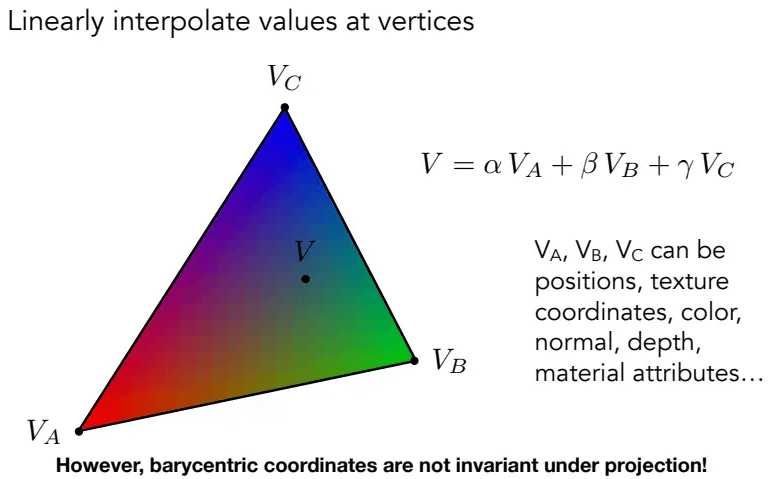
重心坐标系主要用于三角形顶点上属性的插值。

数学定义​

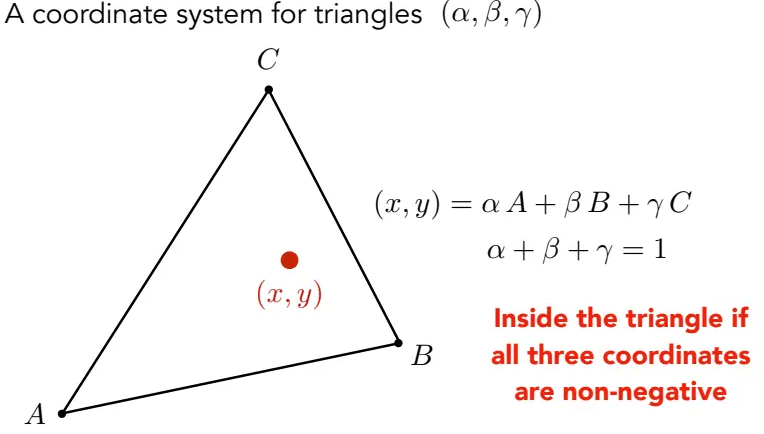
三角形ABC内任一点(x,y)都可以写成上图所示的三点坐标线性组合形式：

  • 当α+β+γ=1\alpha+\beta+\gamma=1时，此时的点(x, y)即为三角形的重心坐标。
  • 当α+β+γ≥0\alpha+\beta+\gamma \geq 0时，点在三角形内。

这三个值可以自成一个坐标系，就是重心坐标系(α,β,γ)(\alpha,\beta,\gamma)。例如，(1,0,0)(1,0,0)所对应的(x,y)(x,y)就是A点。

几何定义​

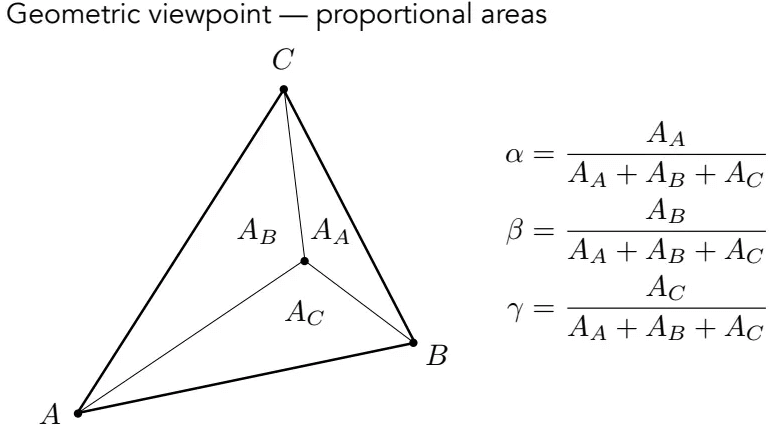
重心坐标可以由面积比求出来：

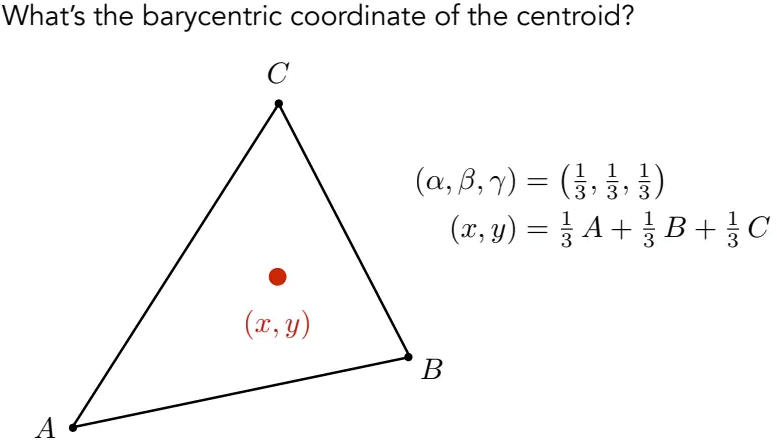
根据三角形重心的几何性质，它平分三个小三角形的面积，则重心的重心坐标为：

重心坐标公式​

插值(interpolation)​

为什么要插值？知道三角形顶点信息，需要在内部各个点之间做平滑过渡。

插值什么内容？纹理坐标，颜色，法向量等等...

重心坐标插值​

插值​

重心坐标可以用来插值，要插值的属性也得是重心坐标的形式(VA,VB,VC)(V_A,V_B,V_C)：

重心坐标虽然简单，但它在投影变换后会发生变化，因此三维空间中，先做好插值工作，然后才通过投影变换转换为二维空间。

透视矫正公式​

(这里还是有点不懂哇)

推导过程详见这里，重心坐标插值下的透视矫正公式如下：

I=Z(α′IAZA+β′IBZB+γ′ICZC)\nonumber I=Z(\alpha'\frac{I_A}{Z_A}+\beta'\frac{I_B}{Z_B}+\gamma'\frac{I_C}{Z_C})

其中各个参数的含义如下：

  • II：屏幕空间三角形内部点的目标属性（颜色，法线，纹理坐标等）。
  • IA, IB, ICI_A,\ I_B,\ I_C：三个顶点的对应属性。
  • ZA, ZB, ZCZ_A,\ Z_B,\ Z_C：三个顶点的 相机空间 的Z值，可由 屏幕空间 的W值得到。
  • α′, β′, γ′\alpha',\ \beta',\ \gamma'：投影变换后，在屏幕空间上算出来的重心坐标。

使用此公式前，还得知道内部点在 相机空间 的Z值ZZ，原理也很简单，就是再用一次此公式，将目标属性变为深度（位于同一二维平面，都是1），有

Z=1α′1ZA+β′1ZB+γ′1ZC\nonumber Z=\frac{1}{\alpha'\frac{1}{Z_A}+\beta'\frac{1}{Z_B}+\gamma'\frac{1}{Z_C}}

然后就能进行任意属性的插值操作了。

线性插值​

线性插值待补充，双线性插值在纹理映射里有提到。

插值​

透视矫正公式​

参考资料​