跳到主要内容

8 - 状态压缩DP

非常哈人动态规划，使我脑子旋转。

概念​

状压 DP 是动态规划的一种，通过将状态压缩为整数来达到优化转移的目的。

例题​

蒙德里安的梦想​

291. 蒙德里安的梦想 - AcWing题库

在摆放方块时，先放横着的，再放竖着的，当我们把横的摆完后，仅需把竖着的填空即可。因此我们只考虑如何摆放横方块就行了，总方案数 = 只放横着的小方块的合法方案数。

那么如何判断当前方案是合法的？需要判断 摆完横的方块后，能不能嵌满竖的方块。可以按列来看，只要每一列内部连续空着的方块是偶数，那么当前方案就合法。

状态表示：

f[i, j]表示已经将前i - 1列摆好，且从第i - 1列伸出到第i列的状态是j的所有方案。我们要求的是方案的数量。

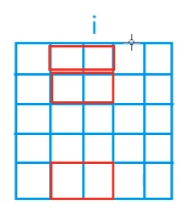
例如下图：

前i - 1列横着的小方块已经放好了，在第i列的第1，2，5行有小方块伸出来。如何把第1、2、5行伸出来的状态存到一个数j里？可以用二进制表示，本例j = 11001。

状态计算：

如何分割集合f[i, j]（通过一步得到f[i, j]）？发现第i-1和i列的方案已经固定了，那么就需要枚举第i-2和i-1列的方案对f[i, j]进行分割，这两列的每一行都有2个选择：伸出来/不伸出来。因此，该状态也能用二进制表示，这里用k表示。

接下来，要把所有合法的方案数添加到f[i, j]里：f[i, j] += f[i - 1, k]。如何判断方案k合法：

  • j & k == 0：如果不为0，说明某一行的两个横着的方块重合了，是非法方案。
  • 所有连续空着的位置的长度必须是偶数，这样才能放入竖方块。

最后讨论边界条件：

  • 初始条件f[0, 0] = 1，什么都不做只需1种方法。
  • 最终答案f[m, 0]，将前m-1列方块摆好，且没有横块伸出来，就是已经把第0 ~ m-1列填满的结果。

参考代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = 12, M = 1 << N;

// 对于状态k, 所有连续空位是不是偶数
vector<int> st(M, 0);
void preCompute(int n)
{
    // 枚举所有状态
    for (int i = 0; i < 1 << n; ++i)
    {
        int cnt = 0, isValid = 1;
        // 枚举状态所有位, 有奇数个0就不合法
        for (int j = 0; j < n; ++j)
        {
            if (i >> j & 1)
            {
                if (cnt & 1)
                {
                    isValid = 0;
                    break;
                }
                cnt = 0;
            }
            else
                cnt++;
        }
        if (cnt & 1)
            isValid = 0;
        st[i] = isValid;
    }
}

// 存储某一列的所有合法状态
vector<vector<int>> states(M);
long long solve(int n, int m)
{
    // 预计算所有状态
    preCompute(n);
    
    // 初始化states
    for (int j = 0; j < 1 << n; ++j)
    {
        states[j].clear();
        for (int k = 0; k < 1 << n; ++k)
        {
            // 将合法状态添加进去
            if ((j & k) == 0 && st[j | k])
                states[j].push_back(k);
        }
    }

    // 状压DP
    vector<vector<long long>> dp(N, vector<long long>(M, 0));
    dp[0][0] = 1;
    for (int i = 1; i <= m; ++i)
        for (int j = 0; j < 1 << n; ++j)
            for (auto k : states[j])
                dp[i][j] += dp[i - 1][k];

    return dp[m][0];
}

int main()
{
    int n, m;
    while (cin >> n >> m, n || m)
        cout << solve(n, m) << '\n';
}

最短Hamilton路径​

91. 最短Hamilton路径 - AcWing题库

状态表示：

f[i, j]，表示所有从节点0走到节点j，且走过的所有点是i（状态压缩）的所有路径。我们要求的是路径的最小值。

状态计算：

如何划分集合f[i, j](仅需一步到达f[i, j])？需要考虑倒数第二个点的情况，假设需要通过点k到达j，有f[i, j] = min(f[除去j的i, k] + a[k, j])。

然后是起点和终点：

  • 对于起点，我们在0处，还没开始走路，路径值为0。因此f[000...1][0] = f[1][0] = 0。
  • 对于终点，是f[(1 << n) - 1][n - 1]，因为起点是0。
  • 要求最小值，其他元素初始化为正无穷。

参考代码如下：

#include <iostream>
#include <vector>
using namespace std;

const int N = 20, M = 1 << N, INF = 1e9;

vector<vector<int>> graph(N, vector<int>(N, 0));
vector<vector<int>> dp(M, vector<int>(N, INF));

int main()
{
    int n;
    cin >> n;
    
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j)
            cin >> graph[i][j];
    
    // dp
    dp[1][0] = 0;
    for (int i = 0; i < 1 << n; ++i)
        for (int j = 0; j < n; ++j)
            // i的第j位为1才有意义(经过j)
            if (i >> j & 1)
            {
                // 枚举所有从k到j的情况
                int withoutJ = i - (1 << j);
                for (int k = 0; k < n; ++k)
                    // withoutJ的第k位为1才有意义(经过k, 不经过j)
                    if (withoutJ >> k & 1)
                        dp[i][j] = min(dp[i][j], dp[withoutJ][k] + graph[k][j]);
            }
            
    cout << dp[(1 << n) - 1][n - 1];
}

练习题​