1 - 排序
准备春招,算法题冲冲冲!
一个有序的输入组合可以减小我们解决问题的难度,有的问题也会在排序的过程中顺带解决,因此排序很重要。
快速排序
如名,它能以很快的速度将一个序列进行排序。但它不是稳定的,如要它稳定,需要给序列每个元素增加“逻辑位置”变量,然后进行双关键字排序。
基于 分治 策略,大体思想如下:
-
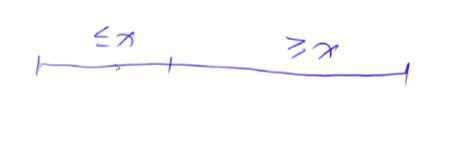
选择分界点:确定一个分界点,使其左边的子序列小于它,右边的子序列大于它。
常见的方法如下:
- 取开头元素
- 取最后一个元素
- 取中间元素
- 取第一个和最后一个之间的随机数等
-
调整区间:[从小到大] 划分两个子区间,使分界点左边的子区间小于等于它,右边的子区间大于它。
-
递归处理:递归处理分界点左右两端。
对于区间的调整,可以使用双指针算法来减少时间和空间复杂度:
- 在序列首尾两侧分别配置指针i,j;
- 只要 i 所指向的元素一直是应该在左边的序列中,i 就一直向右移,直到不符合条件时停止;
- 只要 j 所指向的元素一直是应该在右边的序列中,j 就一直向左移,直到不符合条件时停止;
- 交换 i,j,让序列恢复正常,且两指针都往中间移一位;
- 若 i 和 j 相遇,获得两个排序好的区间。
代码模板
void quickSort(int q[], int l, int r)
{
// 递归出口
if (l >= r) return;
// 1.选择分界点
int mid = q[(l + r) >> 1];
int i = l - 1, j = r + 1;
// 2.调整区间(从小到大)
while (i < j)
{
do i++; while (q[i] < mid);
do j--; while (q[j] > mid);
if (1 < j) std::swap(q[i], q[j]);
}
// 3.递归处理分界点两边
quickSort(q, l, j);
quickSort(q, j + 1, r);
}
快速选择算法
在快速排序的 “调整区间”这一步中,我们会将数据维护成q[l..j-1] < q[j] < q[j + 1..r],此时q[j]左边的元素都比q[j]小,也就知道它的排名。而这样的算法叫做快速选择算法。
来个题看看 215. 数组中的第K个最大元素 - 力扣(LeetCode):
第k个最大元素,也就是升序排序后第n-k个元素,我们在快速选择时,将划分点p和n-k比较,尽量让划分点靠近n-k,直到划分点为n-k,此时划分点就是答案。
参考代码如下:
int quickSelect(vector<int>& nums, int l, int r, int k)
{
// 没必要划分就返回答案
if (l == r)
return nums[k];
// 快排划分
int mid = nums[l + (r - l) / 2];
int i = l - 1, j = r + 1;
while (i < j)
{
do i++; while (nums[i] < mid);
do j--; while (nums[j] > mid);
if (i < j) swap(nums[i], nums[j]);
}
// 比较划分点, 然后再次划分
if (k <= j)
return quickSelect(nums, l, j, k);
else
return quickSelect(nums, j + 1, r, k);
}
int findKthLargest(vector<int>& nums, int k) {
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
习题
785. 快速排序 - AcWing题库
对代码模板的简单运用~
#include <iostream>
#include <vector>
using namespace std
void quickSort(vector<int>& arr, int l, int r)
{
if (l >= r) return;
int x = arr.at((l + r) >> 1);
int i = l - 1, j = r + 1;
while (i < j)
{
do i++; while(arr.at(i) < x);
do j--; while(arr.at(j) > x);
if (i < j) swap(arr.at(i), arr.at(j));
}
quickSort(arr, l, j);
quickSort(arr, j + 1, r);
}
int main()
{
int n;
cin >> n;
vector<int> arr(n, 0);
for (int i = 0; i < n; ++i)
{
cin >> arr.at(i);
}
quickSort(arr, 0, arr.size() - 1);
for (auto& i : arr)
cout << i << " ";
}
786. 第k个数 - AcWing题库
对代码模板的简单运用~
#include <iostream>
#include <vector>
using namespace std;
void quickSort(vector<int>& arr, int l, int r)
{
if (l >= r) return;
int x = arr.at((l + r) >> 1);
int i = l - 1, j = r + 1;
while(i < j)
{
do i++; while (arr.at(i) < x);
do j--; while (arr.at(j) > x);
if (i < j) swap(arr.at(i), arr.at(j));
}
quickSort(arr, l, j);
quickSort(arr, j + 1, r);
}
int main()
{
int n, x;
cin >> n >> x;
vector<int> arr(n);
for (int i = 0; i < n; ++i)
{
cin >> arr.at(i);
}
quickSort(arr, 0, n - 1);
cout << arr.at(x - 1);
}
归并排序
算法思路
基于 分治 策略,大体思想如下:
-
确定分界点: mid = (l+r)/2
-
**递归处理:**递归排序左右两边
-
归并[从小到大]:把两个有序序列合二为一:
- 若两个有序序列全都没有遍历完,则不断比较两个指针的值,较小值进入新数组 res 中,直到其中一个遍历完。
- 将未遍历完的序列剩下的元素进入 res 中。
代码模板
int tmp[n]; // 用于归并的新数组
void mergeSort(int q[], int l, int r)
{
// 递归出口
if (l >= r) return;
// 确定分界点, 然后递归处理两个子序列
int mid = (l + r) >> 1;
mergeSort(q, l, mid);
mergeSort(q, mid + 1, r);
// 归并操作
int i = l, j = mid + 1, k = 0;
// 同时遍历两个子序列, 较小值进入新数组中
while (i <= mid && j <= r)
{
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
// 遍历完其中一个序列, 剩下一个序列进入新数组
while (i <= mid) tmp[k++] = q[i++];
while (j <= mid) tmp[k++] = q[j++];
// 把新数组排序好的元素放回原数组中
for (i = l, k = 0; i <= r; ++i, ++k)
q[i] = tmp[k];
}
习题
787. 归并排序 - AcWing题库
对代码模板的简单应用~
#include <iostream>
#include <vector>
using namespace std;
void mergeSort(vector<int>& arr, int l, int r, vector<int>& tmp)
{
if (l >= r) return;
int mid = (l + r) >> 1;
mergeSort(arr, l, mid, tmp);
mergeSort(arr, mid + 1, r, tmp);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
{
if (arr.at(i) <= arr.at(j))
tmp.at(k++) = arr.at(i++);
else
tmp.at(k++) = arr.at(j++);
}
while (i <= mid) tmp.at(k++) = arr.at(i++);
while (j <= r) tmp.at(k++) = arr.at(j++);
for (i = l, k = 0; i <= r; ++i, ++k)
arr.at(i) = tmp.at(k);
}
int main()
{
int n;
cin >> n;
vector<int> arr(n), tmp(n);
for (int i = 0; i < n; ++i)
cin >> arr.at(i);
mergeSort(arr, 0, n - 1, tmp);
for (auto i : arr)
cout << i << " ";
}
逆序对
788. 逆序对的数量 - AcWing题库
在归并的过程中可以计算逆序对的数量,以输入样例 2 3 4 5 6 1为例:
- 划分子序列:
2 3 4,5 6 1 - 对
2 3 4划分子序列:2 3,4 - 对
2 3划分子序列:2,3 - 归并
2和3,没有逆序对,得到2 3 - 归并
2 3和4,没有逆序对,得到2 3 4 - 对
5 6 1划分子序列:5 6,1 - 对
5 6划分子序列:5,6 - 归并
5和6,没有逆序对,得到5 6 - 归并
5 6和1,发现5和1,6和1是逆序对,得到1 5 6 - 归并
2 3 4和1 5 6,发现2和1,3和1,4和1是逆序对,得到1 2 3 4 5 6。 - 最终有5对逆序对。
也就是说,在归并过程中,左边序列的元素a如果大于右边序列的元素b,那么左边序列a和a以后的元素均大于b,这些元素都和b是逆序对。因此可以得到结论:
逆序对的个数为数次归并过程中mid - i + 1的和。
代码如下:
#include <iostream>
#include <vector>
using namespace std;
// 注意这里cnt的数据类型, 不要太小了
long cnt = 0;
void mergeSort(vector<int>& arr, int l, int r, vector<int>& tmp)
{
if (l >= r) return;
int mid = (l + r) >> 1;
mergeSort(arr, l, mid, tmp);
mergeSort(arr, mid + 1, r, tmp);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
{
if (arr.at(i) <= arr.at(j))
tmp.at(k++) = arr.at(i++);
else
{
tmp.at(k++) = arr.at(j++);
cnt += mid - i + 1;
}
}
while (i <= mid) tmp.at(k++) = arr.at(i++);
while (j <= r) tmp.at(k++) = arr.at(j++);
for (i = l, k = 0; i <= r; ++i, ++k)
arr.at(i) = tmp.at(k);
}
int main()
{
int n;
cin >> n;
vector<int> arr(n), tmp(n);
for (int i = 0; i < n; ++i)
cin >> arr.at(i);
mergeSort(arr, 0, n - 1, tmp);
cout << cnt;
}
类似题目:
-
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
int ans;
void mergeSort(vector<int>& nums, int l, int r, vector<int>& tmp) {
if (l >= r)
return;
int mid = l + (r - l) / 2;
mergeSort(nums, l, mid, tmp);
mergeSort(nums, mid + 1, r, tmp);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (nums[i] <= nums[j]){
ans += j - (mid + 1);
tmp[k++] = nums[i++];
}
else {
tmp[k++] = nums[j++];
}
}
while (i <= mid)
{
ans += j - (mid + 1);
tmp[k++] = nums[i++];
}
while (j <= r)
tmp[k++] = nums[j++];
for (i = l, k = 0; i <= r; ++i, ++k)
nums[i] = tmp[k];
}
int reversePairs(vector<int>& record) {
vector<int> tmp(record.size(), 0);
mergeSort(record, 0, record.size() - 1, tmp);
return ans;
}这里换了一种思路来计算逆序对:
当我们每次将
[l, mid + 1)的数字放到答案数组时,它对逆序对的贡献就是j - (mid + 1)。因为假设在[mid + 1, r]中,j前面有x个比num[j]小的数字,如果现在num[i] <= num[j],就要把num[i]放到比它小的数字后面,而这样的数字有x个,x算出来就是j - (mid + 1)。
315. 计算右侧小于当前元素的个数 - 力扣(LeetCode)
这道题也是找逆序对数量,不过变成了 找每个数它自己逆序对的数量。为了在正确的位置保存每个数的逆序数,需要对数组和下标一起排序,因此有temp.val和temp.index。
参考代码如下:
struct
{
vector<int> val;
vector<int> index;
} temp;
vector<int> index;
vector<int> ans;
void mergeSort(vector<int>& nums, int l, int r)
{
if (l >= r)
return;
int mid = l + (r - l) / 2;
mergeSort(nums, l, mid);
mergeSort(nums, mid + 1, r);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
{
if (nums[i] <= nums[j])
{
temp.index[k] = index[i];
temp.val[k] = nums[i];
ans[index[i]] += j - (mid + 1);
++k, ++i;
}
else
{
temp.index[k] = index[j];
temp.val[k] = nums[j];
++k, ++j;
}
}
while (i <= mid)
{
temp.index[k] = index[i];
temp.val[k] = nums[i];
ans[index[i]] += j - (mid + 1);
++k, ++i;
}
while (j <= r)
{
temp.index[k] = index[j];
temp.val[k] = nums[j];
++k, ++j;
}
for (i = l, k = 0; i <= r; ++i, ++k)
{
index[i] = temp.index[k];
nums[i] = temp.val[k];
}
}
vector<int> countSmaller(vector<int>& nums) {
ans.resize(nums.size());
index.resize(nums.size());
temp.index.resize(nums.size());
temp.val.resize(nums.size());
for (int i = 0; i < nums.size(); ++i)
index[i] = i;
mergeSort(nums, 0, nums.size() - 1);
return ans;
}