信息
文章中可能会出现一些错误,希望大佬们可以在评论区指出错误,感谢支持!
4 - 链表
继续学算法~
合并链表
合并两个有序链表
可以准备一个假的头节点作为合成后链表的头节点,然后像归并排序那样合并有序链表,如果其中一个链表合并完/空了,直接把另一个链表的剩余节点归并。
参考代码如下:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* head = new ListNode(-1);
ListNode* cur = head;
ListNode* cur1 = list1;
ListNode* cur2 = list2;
while (cur1 && cur2)
{
if (cur1->val < cur2->val)
{
cur->next = cur1;
cur1 = cur1->next;
}
else
{
cur->next = cur2;
cur2 = cur2->next;
}
cur = cur->next;
}
if (cur1)
cur->next = cur1;
else if (cur2)
cur->next = cur2;
return head->next;
}
合并k个有序链表
和之前合并两个有序链表类似,但这次链表数量最多高达10^4,如果用暴力循环必定超时。因此可以使用优先队列,存储k个链表的头节点,然后将优先队列队头取出来(别忘了将它的下一个元素入队),加入假头节点链表即可。
算法时间复杂度为,其中k是链表条数,N是链表节点总数。
代码如下:
ListNode* mergeKLists(vector<ListNode*>& lists) {
auto cmp = [](ListNode* v1, ListNode* v2){
return v1->val > v2->val;
};
priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> q;
// 初始化优先队列
for (ListNode* node : lists)
if (node)
q.push(node);
// 开始合并链表
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
while (!q.empty())
{
ListNode* node = q.top();
q.pop();
if (node->next)
q.push(node->next);
cur->next = node;
cur = cur->next;
}
return dummy->next;
}
链表倒数第k个节点
单链表的倒数第k个节点
19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
删除链表的倒数第k个节点,也就是删除链表正数第n-k+1个节点。可以用双指针的方式通过一次遍历得到链表的第X个节点:首先让前驱指针向前走k步,然后让前驱和后继指针同时往前走,直到前驱为空,这样后继指针就指向链表的倒数第k个节点了。
参考代码如下:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(-1);
dummy->next = head;
// 找到倒数第n+1个节点
ListNode* pre = dummy;
ListNode* ne = dummy;
while (n--)
ne = ne->next;
while (ne->next)
{
ne = ne->next;
pre = pre->next;
}
// 删除倒数第n个节点
pre->next = pre->next->next;
return dummy->next;
}
单链表的中点
使用快慢指针,快指针每次走两下,慢指针每次走一下,这样当快指针走完后(碰到空节点),慢指针指向的就是中点了。
参考代码如下:
ListNode* middleNode(ListNode* head) {
ListNode* fast = head, *slow = head;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
判断链表是否包含环
可以用快慢指针解决,如果链表存在环,必然有快慢指针重合的情况(快指针超了慢指针一圈)。参考代码如下:
bool hasCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
return true;
}
return false;
}
这是上面问题的进阶,需要找到环形链表的起点。
当快慢指针相遇时,快指针比慢指针多走了k步,而这个k必定是环长度的倍数。假设相遇点距离起点m步,慢指针走到相遇点用k步,快指针走到相遇点用2k步。那么从头节点到环形链表起点,从相遇点到环形链表起点都需要k-m步。
因此把其中一个指针放到起点,然后让他们同时走1步,直到二者相遇,相遇的地方就是环形链表的起点。
参考代码如下:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
bool isCycle = false;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
isCycle = true;
break;
}
}
if (isCycle)
{
fast = head;
while (fast != slow)
{
fast = fast->next;
slow = slow->next;
}
return fast;
}
else
return nullptr;
}
链表相交
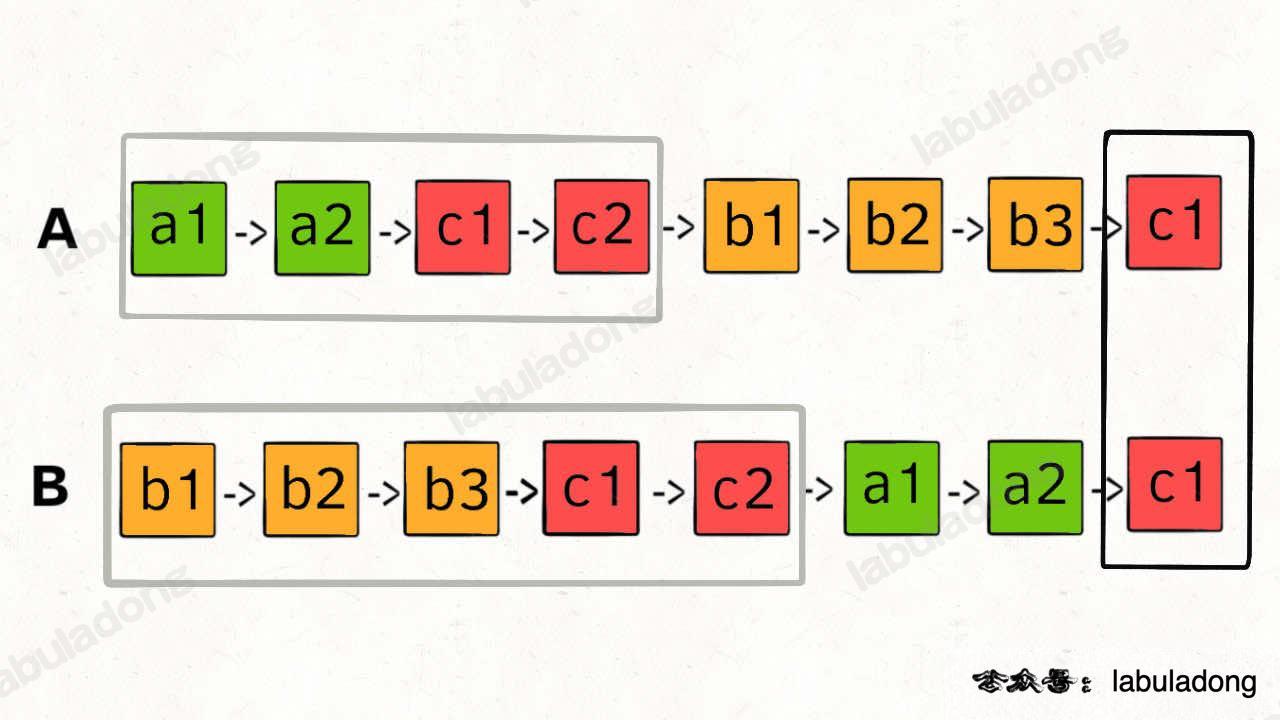
两链表是否相交
如图,A链表遍历完马上遍历B,B链表遍历完马上遍历A,直到它们同时到达相交节点,而这个节点可能有内容(相交了),也有可能是nullptr(不相交)。
参考代码如下:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *pa = headA;
ListNode *pb = headB;
while (pa != pb)
{
pa = pa == nullptr ? headB : pa->next;
pb = pb == nullptr ? headA : pb->next;
}
return pa;
}