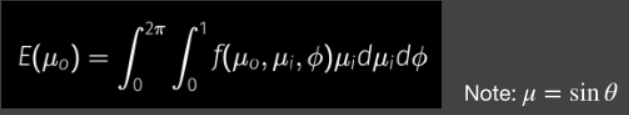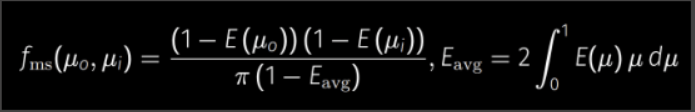跳到主要内容

01 - 基于物理的材质PBR

本文将介绍PBR的概念，以及两种基于物理的材质（微表面BRDF及其着色、迪士尼BRDF）。

PBR和PBR材质​

概念​

PBR，即基于物理的渲染（Physically-Based Rendering），是指在渲染过程中，有关材质、光照、相机、光传输等都要基于准确的物理定律。因此PBR不只是材质，不过人们通常认为PBR就是基于物理的材质。

实时渲染中的PBR​

在实时渲染中，PBR比离线渲染的效果要差一些，而且也不是严格的“基于物理”：

  • 对于普通的物体表面，常用 **微表面模型(Microfacet models)**和 迪士尼原则BRDF(Disney principled BRDFs)。前者虽然是PBR，但经常被错误使用；后者是针对艺术家定义的，不是PBR。
  • 对于体素上的参与介质（云、烟雾、头发等），需要快且近似计算光的单次和多次散射。

在RTR领域中，性能是最重要的，不要搞错方向。

微表面BRDF​

概念​

微表面模型是一种基于物理的局部光照模型，它假设物体的微表面是凹凸不平的，因此微表面法线分布各不相同。

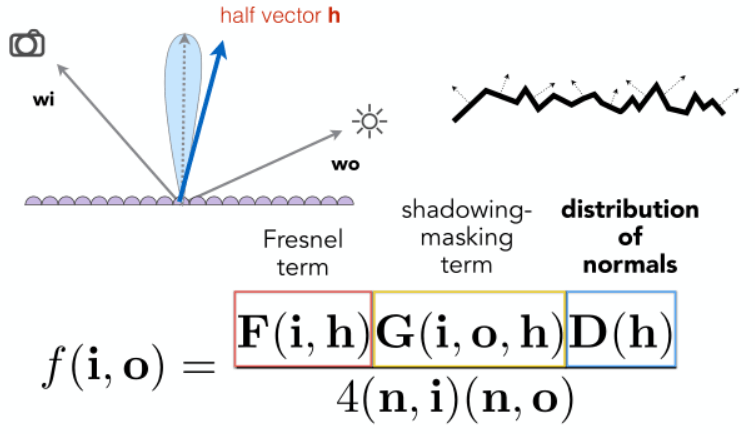
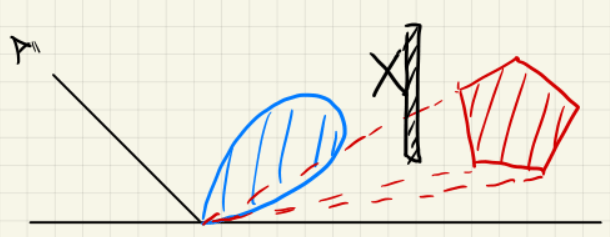
如图，微表面BRDF一共有三项：

  • F项：菲涅尔项，描述物体表面反射光线的比例是依赖于光线的入射角和偏振这一现象。
  • G项：阴影遮蔽项，由于微表面会发生自遮挡现象，该项用于对着色结果进行部分变暗修正。
  • D项：法线分布项，决定有多大比例的微表面法线朝向h。

接下来详细了解一下。

菲涅尔项 F​

如图，菲涅尔项(Fresnel Term) 描述了物体表面反射光线的比例是依赖于光线的入射角和偏振/极化这一现象。随着观察角度（法线和视线的夹角）增大，桌面上反射物体就越清楚：

可以发现，如果要直接准确计算菲涅尔项会很麻烦，可以用Schlick近似去快速计算菲涅尔项的大概值。

Ps：Schlick近似对金属材质的效果有误差，Hoffman近似对其进行拓展，让它支持表示金属材质。

法线分布函数 D/NDF​

法线分布函数(Normal Distribution Function)，表示微表面法线的分布情况，当微表面法向量和半程向量方向完全一致时，入射光才能反射出去。

两种结果​

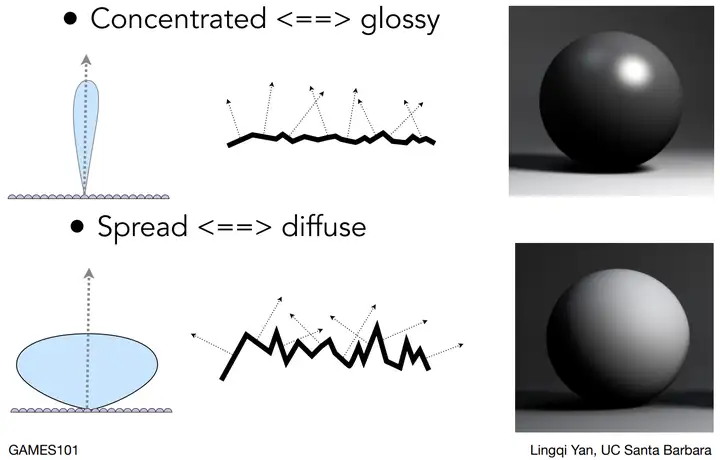
如图：

  • 法线分布越集中，说明物体表面越光滑（glossy）；
  • 法线分布越分散，说明物体表面越粗糙（diffuse）。

常见NDF模型​

目前常见的NDF模型有Beckmann模型，GGX模型等。为了描述球面上的法线分布，可以先将这些法线用球面立体角投影到单位圆上。

Beckmann模型​

它可以描述不同粗糙程度的表面，类似高斯函数，但它定义在 坡度空间(Slope space) 上，定义域有限，而高斯函数定义域是无限的。

如图，α\alpha描述物体表面的粗糙程度，越小越光滑；θh\theta_h是半程向量和法线的夹角。分母是为了让该模型在 球面立体角投影上能过归一化。

GGX模型​

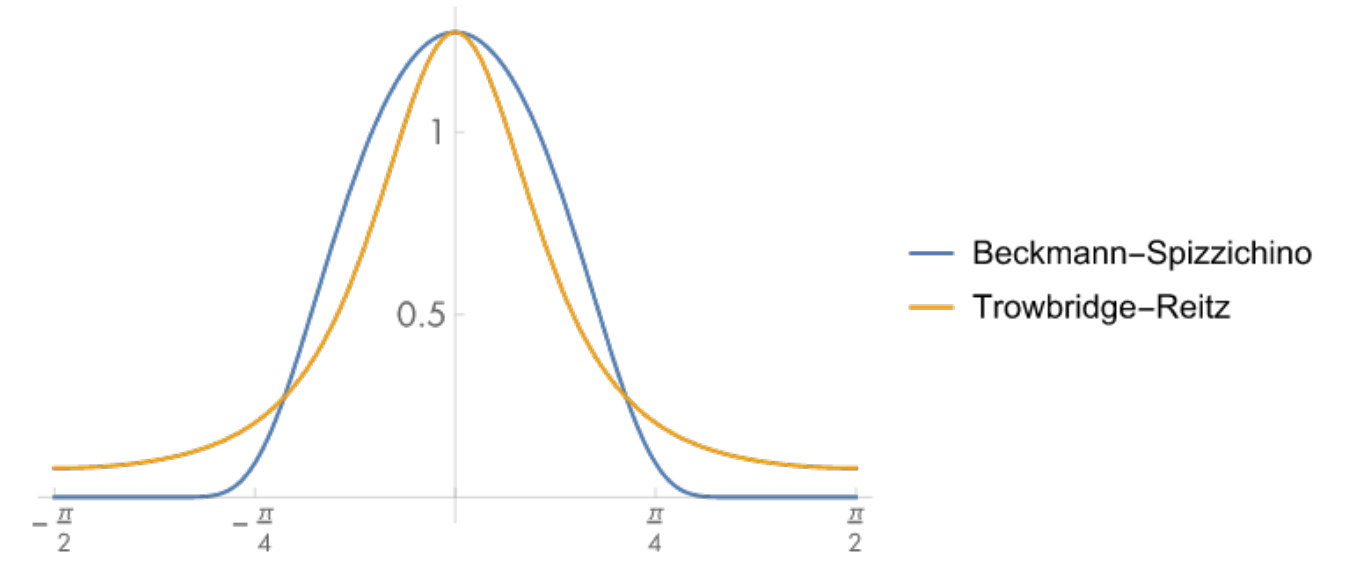
GGX模型，也称Trowbridge-Reitz模型，它的公式如下：

DGGX(h)=α2πcos⁡4θh(α2+tan⁡2θh)2\nonumber D_{\mathrm{GGX}}\left(h\right)=\frac{\alpha^2}{\pi\cos^4\theta_h\left(\alpha^2+\tan^2\theta_h\right)^2}

如图，GGX模型的特点就是“长尾”，它在衰减到一定位置的时候，值还不为0。因此相较于Backmann模型有边缘光柔和/光晕效果：

GTR模型​

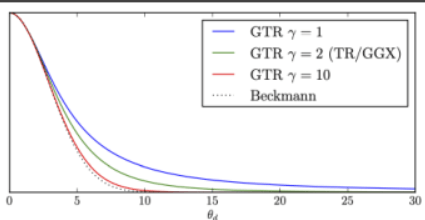
是GGX模型的拓展，相较于GGX更加通用，有“更长的尾”，由参数γ\gamma控制：

DGTR(h)=c(α2cos⁡2θh+sin⁡2θh)γ\nonumber D_{\text{GTR}}\left(h\right)=\frac{c}{\left(\alpha^2\cos^2\theta_h+\sin^2\theta_h\right)^\gamma}

当γ=2\gamma=2时，GTR模型便退化为GGX模型。

阴影遮蔽/几何项 G​

阴影遮蔽项(Shadow-Masking Term)，又称 几何项(Geometry Term)。由于微表面反射光线时会发生自遮挡现象，此项会依据微表面的几何分布，对着色结果进行“变暗”修正。

自遮挡现象

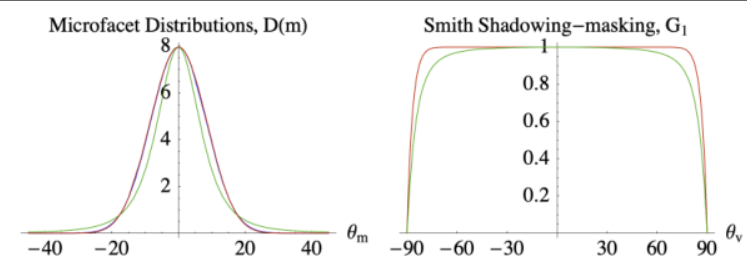
常用Smith Shadowing-masking项作为G项，它假设法线分布为某种统计学分布，根据这种分布将阴影遮蔽项拆分为阴影项和遮蔽项：

G(ωi,ωo,h)=G1(ωi,h)G1(ωo,h)\nonumber G\left(\omega_{i},\omega_{o},h\right)=G_{1}\left(\omega_{i},h\right)G_{1}\left(\omega_{o},h\right)

由于微表面BRDF仅考虑光线弹射一次的情况，随着材质的粗糙度提高，着色结果会越来越暗，发生“能量损失”：

因此也要考虑光在微表面进行多次弹射的情况，以补足“损失的能量”。

Kulla-Conty近似​

工业界上提出 Kulla-County近似 这一方法，它通过经验性的方式去补全多次“损失的能量”，且在RTR领域效率不错。

要想计算一次弹射损失的能量，就得先计算有多少能量被反射出来：

假设总的能量是1，那么损失的能量就是1−E(μO)1-E(\mu_O)。考虑到对称性，有入射损失的能量就会有出射损失的能量，那么最后的答案一定是基于c(1−E(μi))(1−E(μO))c(1-E(\mu_i))(1-E(\mu_O))形式。

这里直接给出C是什么，以及一次弹射后的公式：

其中，E(μ)E(\mu)和EavgE_{avg}可以预计算，并存储到一张二维纹理中：

应用Kulla-Conty近似后的结果如下：

上面只说明了物体表面没有颜色的情况，如果物体表面有颜色该怎么办？可以先按没有颜色的情况算，然后再加上由于颜色引起的能量损失。

先引入平均F项的定义：

Favg=∫01F(μ)μdμ∫01μdμ=2∫01F(μ)μdμ\nonumber F_{\mathrm{avg}}=\frac{\int_0^1F(\mu)\mu\mathrm{d}\mu}{\int_0^1\mu\mathrm{d}\mu}=2\int_0^1F(\mu)\mu\mathrm{d}\mu

即不管入射角多大，求平均反射了多少能量。

接下来分情况讨论：

  • 可以直接看到的能量：FavgEavgF_{avg}E_{avg}
  • 经过一次弹射能看到的能量：Favg(1−Eavg)⋅FavgEavgF_{avg}(1-E_{avg})·F_{avg}E_{avg}​
  • ...
  • 经过k次弹射能看到的能量：Favgk(1−Eavg)k⋅FavgEavgF_{avg}^k(1-E_{avg})^k·F_{avg}E_{avg}

将这些能量加起来，就得到一个级数：

FavgEavg1−Favg(1−Eavg)\nonumber \frac{F_{\mathrm{avg}}E_{\mathrm{avg}}}{1-F_{\mathrm{avg}}(1-E_{\mathrm{avg}})}

将它乘到没颜色的BRDF上就行了。

可见效果还是不错的。

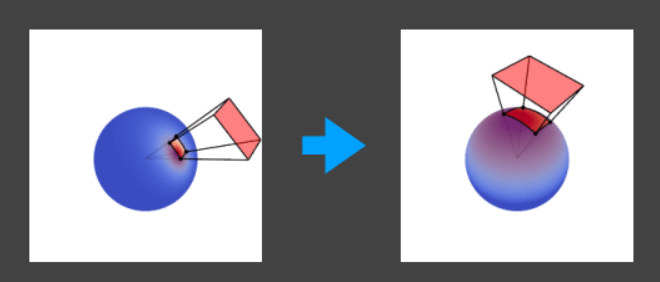
使用LTC计算着色​

LTC（Linearly Transformed Cosines），即线性变换余弦，常用于微表面模型着色的相关计算中。

限制​

  1. 主要针对GGX的法线分布，但其他分布也可以
  2. 不考虑阴影，即不考虑遮挡
  3. 光源是多边形的

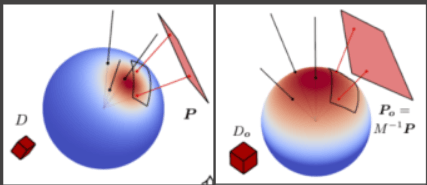
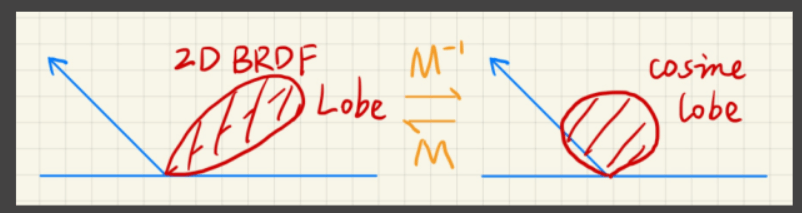
思路​

出射的BRDF反射波瓣可变换为一个余弦函数，多边形光源的形状也能跟着变换。变换后的BRDF有解析解。

可以定义一个变换MM：

  • BRDF通过M−1M^{-1}变换为余弦函数；
  • 所有方向ωi\omega_i通过M−1M^{-1}变换成ωi′\omega_i'；
  • 多边形光源PP通过M−1M^{-1}变换成P′P'

做法​

假设LiL_i相同，把BRDF和Cos项合并后的渲染方程如下：

L(ωo)=Li⋅∫PF(ωi)dωi\nonumber L(\omega_o)=L_i\cdot\int_PF(\omega_i)\mathrm{d}\omega_i

然后进行LTC变换，将ωi′\omega_i'经过MM变换到ωi\omega_i，有ωi=Mωi′∥Mωi′∥\omega_i=\frac{M\omega_i'}{\|M\omega_i'\|}，代入渲染方程后如下：

L(ωo)=Li⋅∫Pcos⁡(ωi′)dMωi′∥Mωi′∥\nonumber L(\omega_o)=L_i\cdot\int_P\cos(\omega_i')\mathrm{d}\frac{M\omega_i'}{\|M\omega_i'\|}

最后引入J，简化有：

L(ωo)=Li⋅∫P′cos⁡(ωi′)J dωi′\nonumber L(\omega_o)=L_i\cdot\int_{P^{\prime}}\cos(\omega_i^{\prime})J\mathrm{~d}\omega_i^{\prime}

迪士尼BRDF​

由于微表面BRDF不擅长表示真实材质/多层材质，且对艺术家不友好，迪士尼规则的BRDF便诞生了。

设计原则​

它的设计原则如下：

  • 使用直观的参数，而不是物理参数来控制模型呈现的效果；
  • 模型使用的参数尽可能的少；
  • 参数的合理范围应该是从 0 到 1；
  • 在必要时，即使参数的取值超出了 [0,1] 范围，也能得到有意义的结果；
  • 所有的参数组合应该尽可能的稳健和合理；

具体参数​

  • 次表面散射：值越大，看起来越平
  • 金属度
  • 高光度
  • 高光tint：决定高光反射出的颜色，0~1由无色逐渐变为物体本身颜色。
  • 粗糙度
  • 各向异性程度
  • Sheen：模拟纺织物边缘绒毛的明亮效果。
  • ClearCoat：模拟清漆效果

优缺点​

优点：

  • 容易理解和使用
  • 可以表示的材质种类繁多
  • 有开源实现

缺点：

  • 不是基于物理的
  • 需要的参数空间很大

参考资料​