跳到主要内容

07 - 四元数

定义​

四元数的定义和复数类似，它有1个实部和3个虚部：

q=a+bi+cj+dk,(a,b,c,d∈R)\nonumber q=a+bi+cj+dk, \quad (a,b,c,d \in \mathbb{R})

并且

i2=j2=k2=ijk=−1\nonumber i^2=j^2=k^2=ijk=-1

我们经常将四元数的实部和虚部分开，并用一个三维向量来表示虚部：

q=[s, v](v=[xyz], s,x,y,z∈R)\nonumber q=[s,\ \mathbf{v}] \quad (\mathbf{v}= \begin{bmatrix} x\\ y\\ z \end{bmatrix}, \, s,x,y,z \in \mathbb{R})

性质​

模长/范数​

四元数的模长/范数(Norm)/大小的定义是：

∥q∥=∥[s, v]∥=s2+∥v∥2=s2+v⋅v=∥[s, (x,y,z)]∥=s2+s2+y2+z2\begin{align} \nonumber \|q\| &= \|[s,\,\mathbf{v}]\| = \sqrt{s^2+\|\mathbf{v}\|^2} = \sqrt{s^2 + \mathbf{v·v}} \\ \nonumber &= \|[s,\,(x,y,z)]\| = \sqrt{s^2+s^2+y^2+z^2} \end{align}

加减法​

只需将分量相加/减就行：

q1±q2=[s±t, v±u]\nonumber q_1 \pm q_2 = [s\pm t,\, \mathbf{v} \pm \mathbf{u}]

乘法​

首先是四元数与标量的乘法，只需将标量乘到四个分量上就行，遵守交换律。

然后是四元数之间的乘法，它 不遵守交换率，但遵守结合律和分配律：

  • 类复数表示的角度。四元数q1=a+bi+cj+dkq_1=a+bi+cj+dk和q2=e+fi+gj+hkq_2=e+fi+gj+hk的乘积q1q2q_1q_2​为：
q1q2=(a+bi+cj+dk)(e+fi+gj+hk)=(ae−bf−cg−dh)+ (be+af−dg+ch)i+ (ce+df+ag−bh)j+ (de−cf+bg+ah)k\begin{align} \nonumber q_1q_2 &= (a+bi+cj+dk)(e+fi+gj+hk) \\ \nonumber &= (ae-bf-cg-dh)+ \\ \nonumber &\quad\ (be+af-dg+ch)i+ \\ \nonumber &\quad\ (ce+df+ag-bh)j+ \\ \nonumber &\quad\ (de-cf+bg+ah)k \end{align}
  • 向量表示的角度。四元数q1=[w1, v1]q_1=[w_1,\,\mathbf{v_1}]和q2=[w2, v2]q_2=[w_2,\,\mathbf{v_2}]的乘积q1q2q_1q_2为：
q1q2=[w1w2−v1⋅v2, w1v2+w2v1+v1×v2]\nonumber q_1q_2=[w_1w_2-\mathbf{v_1}·\mathbf{v_2}, \,w_1\mathbf{v_2}+w_2\mathbf{v_1}+ \mathbf{v_1}\times\mathbf{v_2}]

还有四元数的点积：

q1⋅q2=w1w2+v1⋅v2\nonumber q_1·q_2=w_1w_2+\mathbf{v_1}·\mathbf{v_2}

共轭和逆​

四元数的共轭表示为q∗q^*，是通过将四元数的矢量部分变负得到的。例如四元数q=[w, v]q=[w,\,\mathbf{v}]的共轭为：

q∗=[w, −v]\nonumber q^*=[w,\,-\mathbf{v}]

并且有

qq∗=q∗q=∥q∥2\nonumber qq^*=q^*q=\|q\|^2

四元数的逆表示为q−1q^{-1}，定义为四元数的共轭除以其大小：

q−1=q∗∥q∣∣\nonumber q^{-1}=\frac{q^*}{\|q||}

并且有

qq−1=[1, 0]\nonumber qq^{-1}=[1,\,\mathbf{0}]

其中[1, 0][1,\,\mathbf{0}]是 单位四元数，因为它的模长是1，可以发现，单位四元数的q−1=q∗q^{-1}=q^*​。

除此之外，两个四元数a, ba,\,b的“差”（这里指变换的差距）为：

d=ba−1\nonumber d=ba^{-1}

对数(log)​

定义四元数p=[cos⁡(θ/2), sin⁡(θ/2)n^]p=[\cos(\theta/2),\,\sin(\theta/2)\mathbf{\hat{n}}]（表示绕n^\mathbf{\hat{n}}旋转θ\theta°），那么它的对数就是

log⁡p=[0, (θ/2)n^]\nonumber \log p=[0,\, (\theta/2)\mathbf{\hat{n}}]

指数(exp)​

定义四元数p=[0, (θ/2)n^]p=[0,\, (\theta/2)\mathbf{\hat{n}}]，则它的指数是

exp⁡p=[cos⁡(θ/2), sin⁡(θ/2)n^]\nonumber \exp p = [\cos(\theta/2),\,\sin(\theta/2)\mathbf{\hat{n}}]

幂运算​

例如四元数qq的t次幂可以被表示为qtq^t，一个单位四元数的t次幂等同于将它的旋转角度缩放至t倍。例如，如果qq表示围绕x轴顺时针旋转30°，那么q2q^2表示围绕x轴顺时针旋转60°。

四元数使用最短弧表示角度位移，不能表示多圈旋转。q8q^8不会绕x轴顺时针旋转240°，而是逆时针旋转120°。也就是说，四元数只会在意最终结果，而不在意过程。

在数学上，四元数的取幂公式如下：

qt=exp⁡(tlog⁡q)\nonumber q^t=\exp(t\log q)

插值​

球面线性插值Slerp​

四元数的球面线性插值（Spherical Linear Interpolation）很有用，因为它允许在两个四元数之间平滑插值，它的定义如下：

Slerp(q0, q1, t)\nonumber \mathrm{Slerp}(q_0,\,q_1,\,t)

q0q_0是插值的起始四元数，q1q_1是插值的结束四元数，t是[0, 1][0,\,1]间的变量，表示插值的距离因子，例如t=0时，结果就是q0q_0。

知道Slerp的定义后，接下来就要推导它的公式了。

从q0q_0到q1q_1，它俩角位移的差值为

Δq=q1q0−1\nonumber \Delta q=q_1q_0^{-1}

然后根据幂运算，取这个差值的一小部分

(Δq)t\nonumber (\Delta q)^t

最后利用四元数乘法让四元数的范围限定到起始四元数和结束四元数间

(Δq)tq0\nonumber (\Delta q)^tq_0

就能得到Slerp的公式了：

Slerp(q0, q1 t)=(q1q0−1)tq0\nonumber \mathrm{Slerp(q_0,\,q_1\,t)} = (q_1q_0^{-1})^tq_0

这是理论上的公式，但它的计算不仅涉及到多个四元数的乘法，而且还包括幂运算，在实际应用中的效率很低。

为了方便理解，直接从几何的角度出发，推导2D向量的Slerp公式，如图：

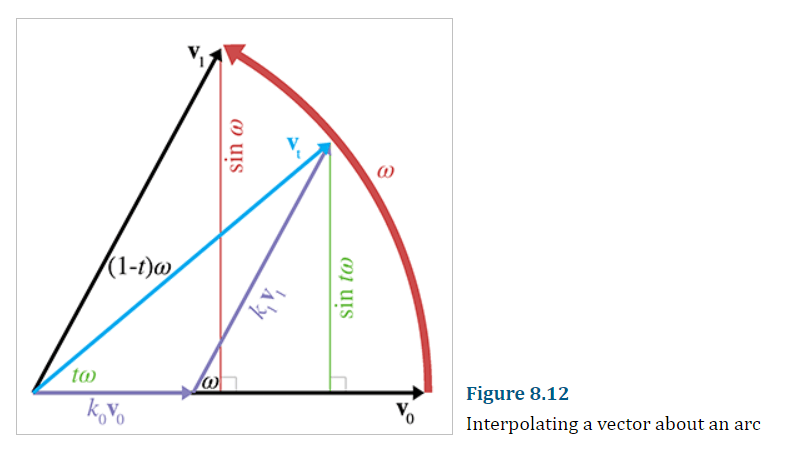
可用发现，vt=k0v0+k1v1\mathbf{v_t}=k_0\mathbf{v_0}+k_1\mathbf{v_1}，接下来就要想法儿确定k0, k1k_0,\,k_1的值了。

在以k1v1k_1\mathbf{v_1}为斜边的直角三角形中，有

sin⁡w=sin⁡twk1\nonumber \sin w=\frac{\sin tw}{k_1}

那么

k1=sin⁡twsin⁡w\nonumber k_1=\frac{\sin tw}{\sin w}

同理可得

k0=sin⁡(1−t)wsin⁡w\nonumber k_0=\frac{\sin(1-t)w}{\sin w}

因此

Slerp(v0,v1,t)=k0v0+k1v1=sin⁡(1−t)wsin⁡wv0+sin⁡twsin⁡wv1\begin{align} \nonumber \mathrm{Slerp(\mathbf{v_0},\mathbf{v_1},t)} &= k_0\mathbf{v_0}+k_1\mathbf{v_1} \\ \nonumber &= \frac{\sin(1-t)w}{\sin w}\mathbf{v_0}+ \frac{\sin tw}{\sin w}\mathbf{v_1} \end{align}

类似的，我们最终得到实际的四元数Slerp公式：

Slerp(q0,q1,t)=sin⁡(1−t)wsin⁡wq0+sin⁡twsin⁡wq1\nonumber \mathrm{Slerp(q_0,q_1,t)} = \frac{\sin(1-t)w}{\sin w}q_0+ \frac{\sin tw}{\sin w}q_1

这样就得到实际运算时用到的四元数Slerp公式了。其中，w=cos⁡−1(q0⋅q1)w=\cos^{-1}(q_0·q_1)。

观察式子不难发现，当q0,q1q_0,q_1非常接近，即ww很小的时候，可能会导致除以0的问题。因此，这种情况下要使用简单的正规化线性插值。

正规化线性插值Nlerp​

四元数的线性插值公式如下：

qt=Lerp(q0,q1,t)=(1−t)q0+tq1\nonumber q_t=\mathrm{Lerp}(q_0,q_1,t)=(1-t)q_0+tq_1

但插值结果却不是单位四元数，我们需要将它除以它的模长，就能转换为单位四元数了，这种插值方法就是正规化线性插值：

Nlerp(q0,q1,t)=(1−t)q0+tq1∥(1−t)q0+tq1∥\nonumber \mathrm{Nlerp}(q_0,q_1,t)=\frac{(1-t)q_0+tq_1}{\|(1-t)q_0+tq_1\|}

但线性插值的角速度变化并不像Slerp那样均匀。

转换为矩阵​

公式如下：

w+xi+yj+zk≡[w−zyxzw−xy−yxwz−x−y−zw]\nonumber w+xi+yj+zk \equiv \begin{bmatrix} w & -z & y & x \\ z & w & -x & y \\ -y & x & w & z \\ -x & -y & -z & w \end{bmatrix}

参考资料​