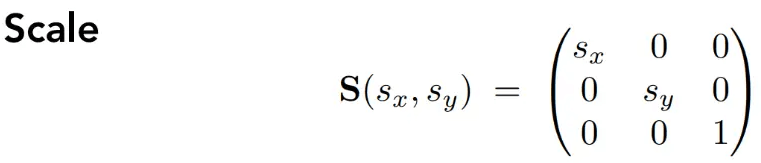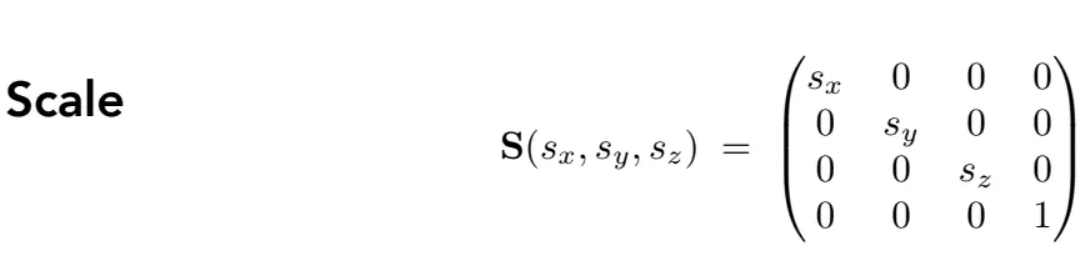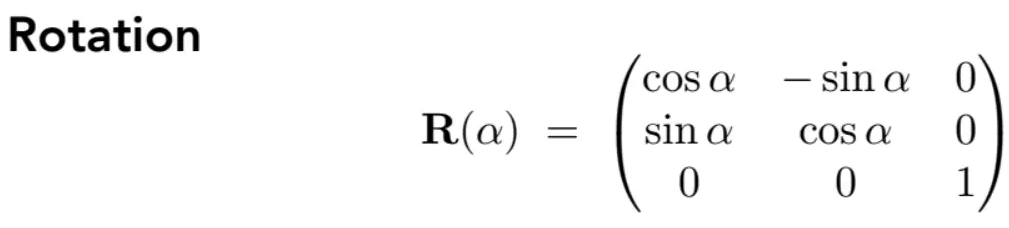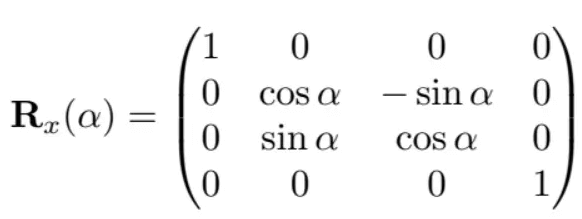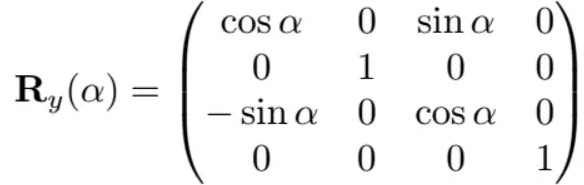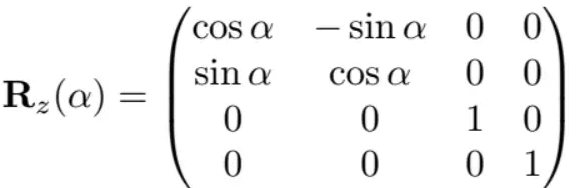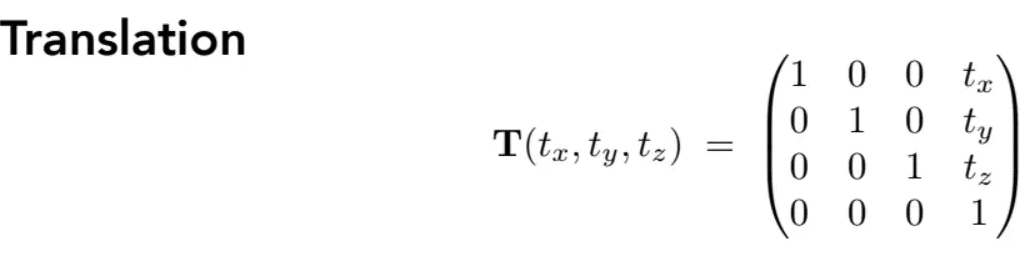齐次坐标(Homogeneous Coordinate)
给点和向量的描述升一维(w),以2D为例:
- 二维中的点:(x,y,1)T
- 二维中的向量:(x,y,0)T
这里理解一下为什么点的w=1,向量的w=0。
在三维中w=1处的标准二维平面,实际的二维点此时表示为(x,y,1)。而对于那些不在w=1平面的点,则可以通过除以w,将它们投影到w=1平面上。这样,齐次坐标(x,y,w)就能够映射到实际的二维点(x/w,y/w):
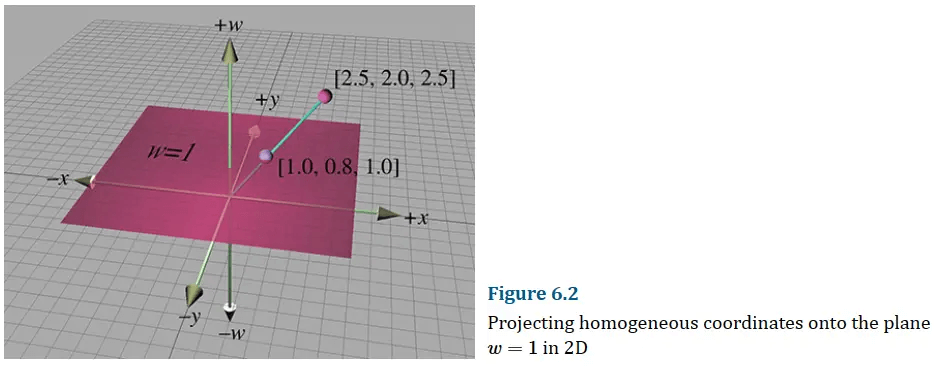
对于任何给定的二维点(x,y),在三维齐次空间中存在无限数量的对应点(kx,ky,k),k=0。这些点形成一条穿过三维齐次空间原点的直线。
当w=0时,上面的除法未定义,而向量恰好没有在空间中平移的概念(都一样),因此可以用来描述向量。
并且根据w的特性,可以快速判别两个点/向量的关系:
- 向量+向量=向量 (0+0=0)
- 点-点=向量(1-1=0)
- 点+向量=点(1+0=1)
- 点+点=中点(1+1=2 表示点(x/2,y/2,1)T)
线性变换(Linear)
形如{x′=ax+byy′=cx+dy的变换,即[x′y′]=[acbd][xy]。包括下面的缩放,反射,错切和旋转。
缩放(Scale)
首先是沿主轴方向的缩放:
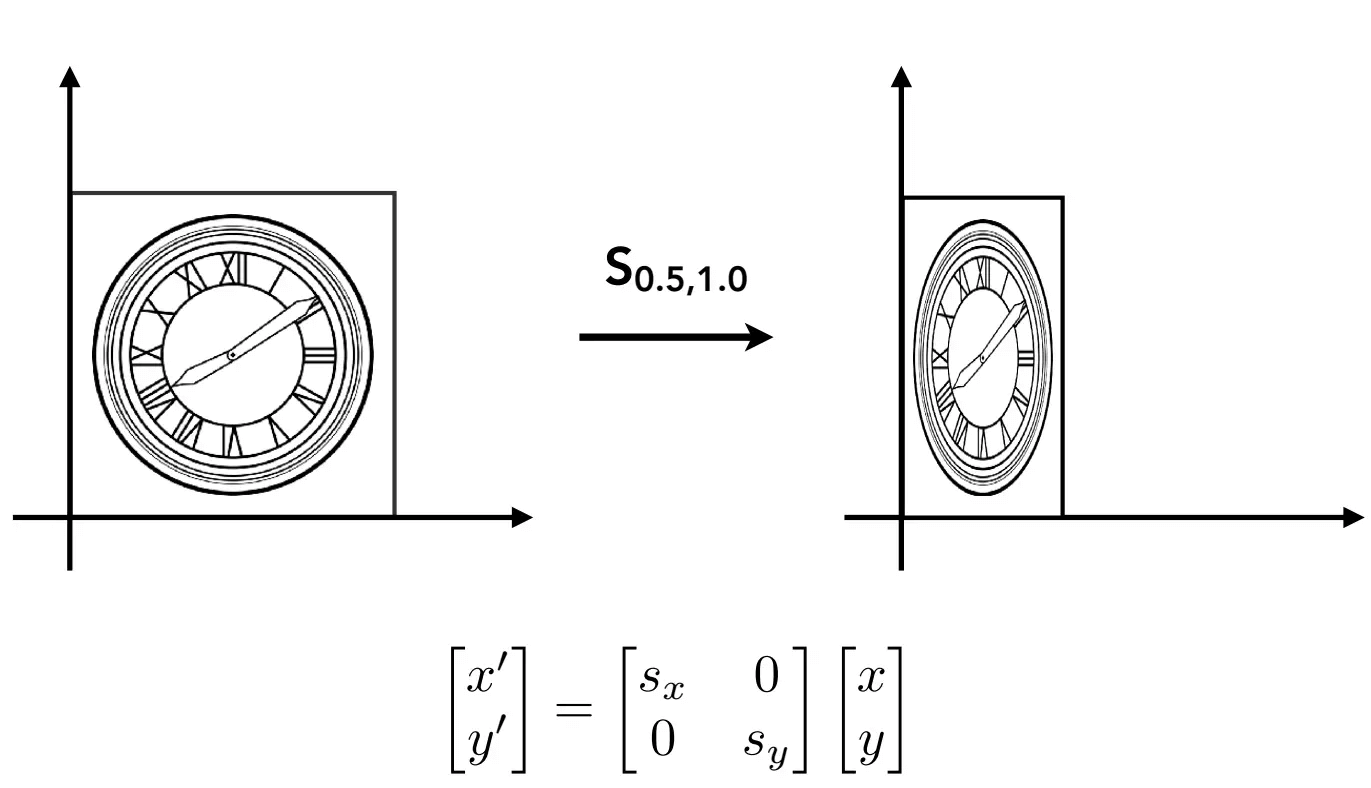
然后是沿任意方向的缩放,该矩阵将在由单位向量n^指定的任意方向上按照k的因子缩放:
S(n^,k)=[1+(k−1)nx2(k−1)nxny(k−1)nxny1+(k−1)ny2]
如果需要引入齐次坐标,简单升维即可:
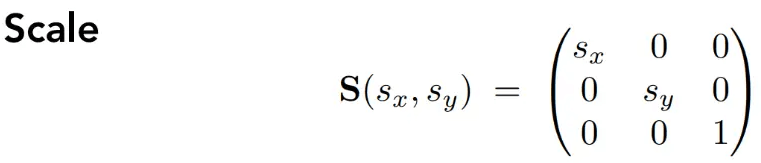
首先是沿主轴方向的缩放,引入齐次坐标:
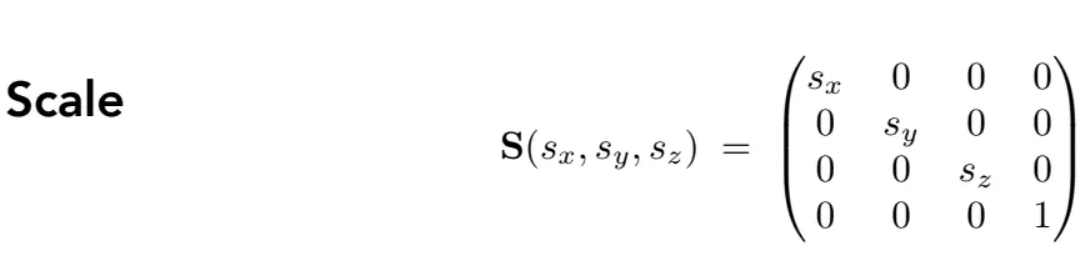
然后是沿任意方向的缩放:
S(n^,k)=1+(k−1)nx2(k−1)nxny(k−1)nxnz(k−1)nxny1+(k−1)ny2(k−1)nynz(k−1)nxnz(k−1)nynz1+(k−1)nz2
反射(Reflection)
反射,也被称为镜像(Mirroring),是一种围绕直线(二维)或平面(三维)中”翻转“对象的变换。
在二维中,可以通过应用-1的比例因子来完成反射。设n^是二维单位矢量,围绕穿过原点并垂直于n^的反射矩阵如下:
R(n^)=S(n^,−1)=[1+(−1−1)nx2(−1−1)nxny(−1−1)nxny1+(−1−1)ny2]=[1−2nx2−2nxny−2nxny1−2ny2]
例如如果向按+y方向反射(即按+x方向缩放-1),它的n^=[1,0]:
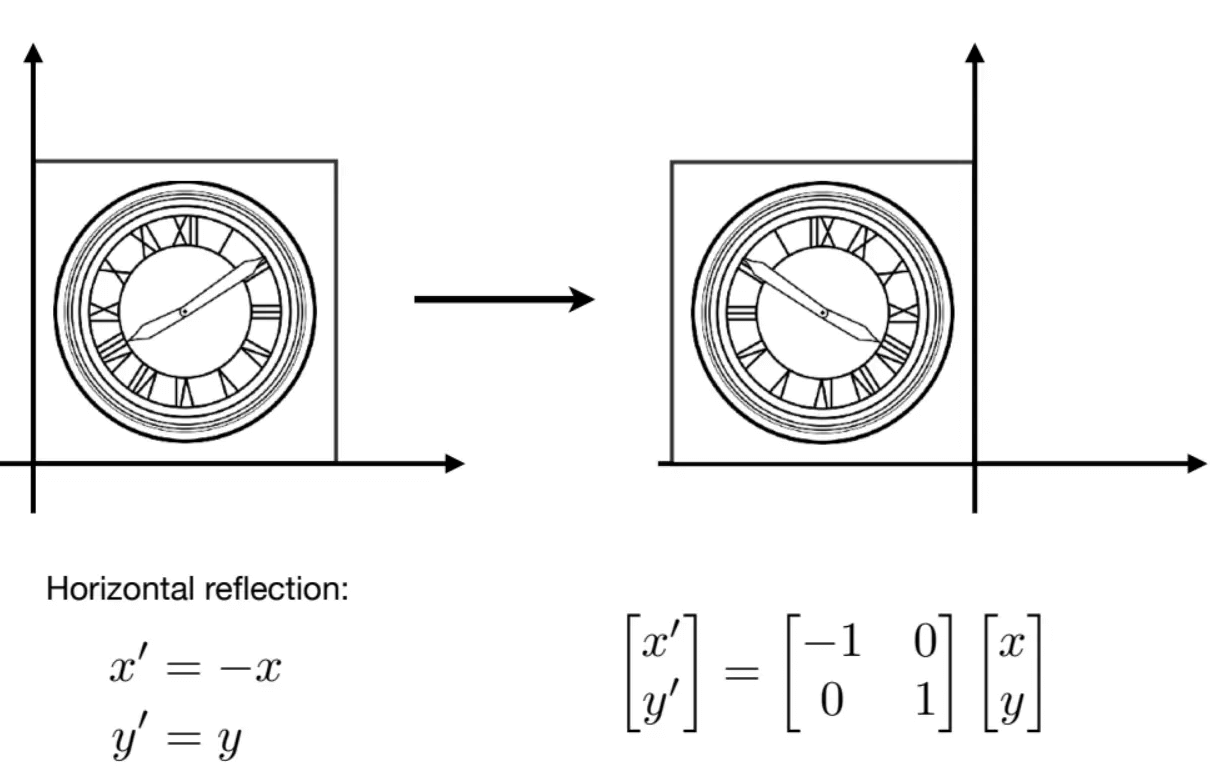
同理,三维中,
R(n^)=S(n^,−1)=1+(−1−1)nx2(−1−1)nxny(−1−1)nxnz(−1−1)nxny1+(−1−1)ny2(−1−1)nynz(−1−1)nxnz(−1−1)nynz1+(−1−1)nz2=1−2nx2−2nxny−2nxnz−2nxny1−2ny2−2nynz−2nxnz−2nynz1−2nz2
错切(Shear)
错切是一种”倾斜“坐标空间的变形,它将不均匀地拉伸坐标空间,不保留角度,但保留了面积/体积。其基本思路是将一个坐标的倍数添加到另一个坐标上。
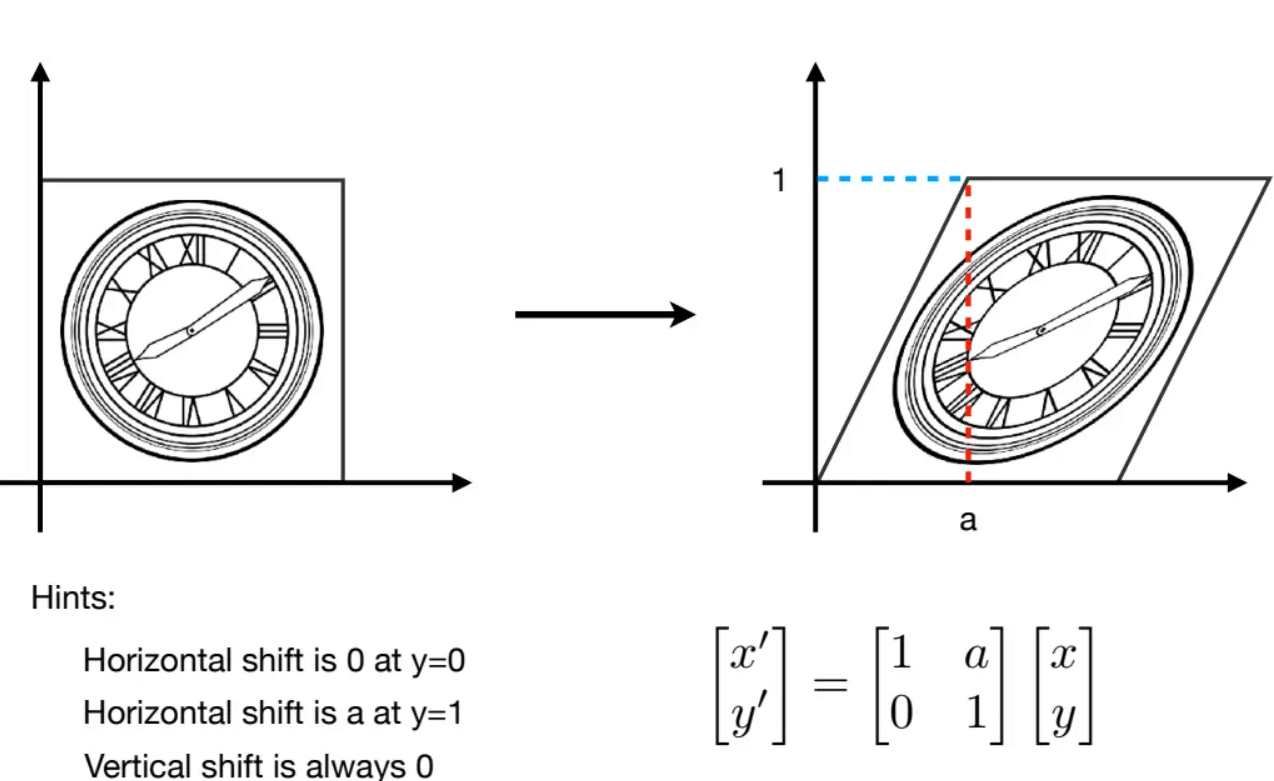
y方向上的同理。
Hxy(s,t)表示x坐标和y坐标按照另一个坐标z移动,即(x' = x + sz, y' = y + tz):
Hxy(s,t)=100010st1Hxz(s,t)=100s1t001Hyz(s,t)=1st010001
旋转(Rotate)
在二维中,只能进行绕某点旋转的变换。以绕原点,逆时针旋转为默认,矩阵如下:
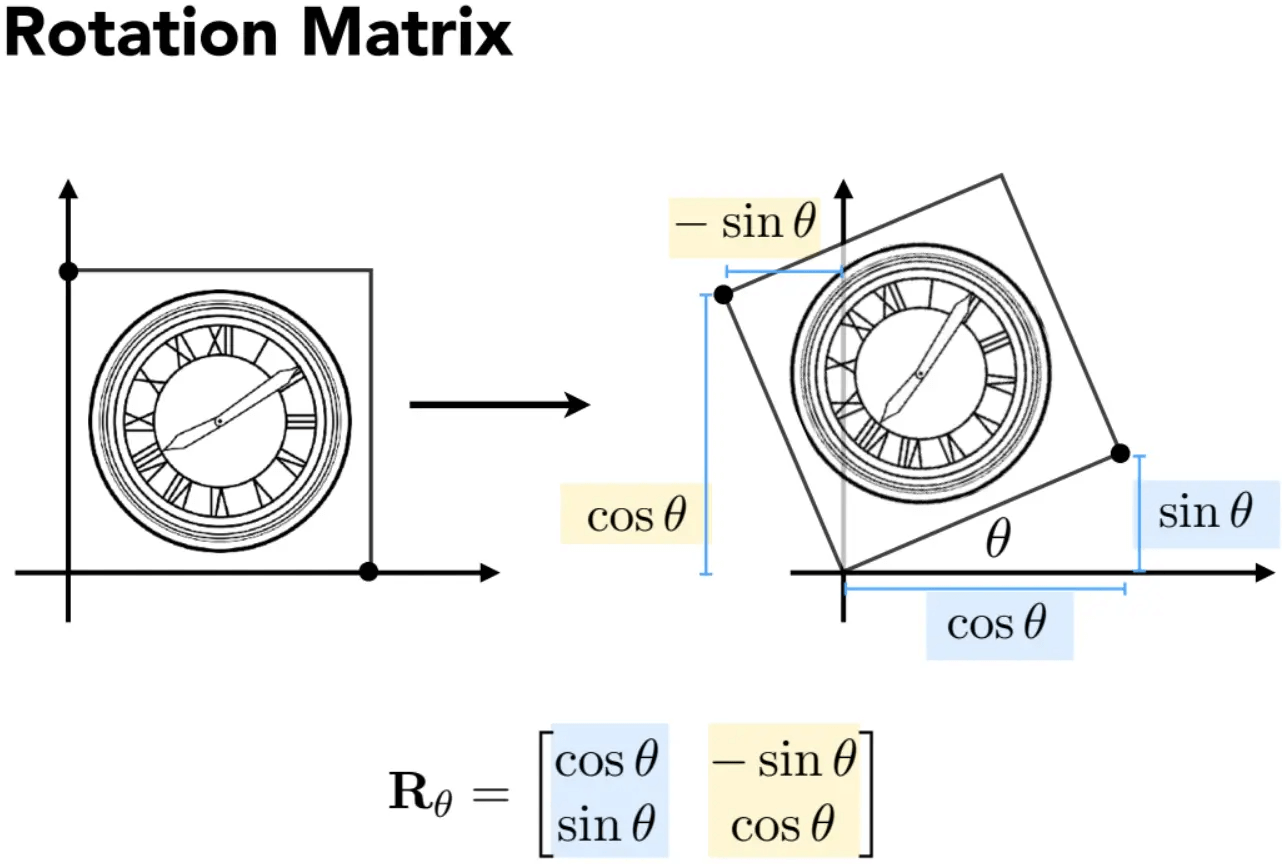
引入齐次坐标系:
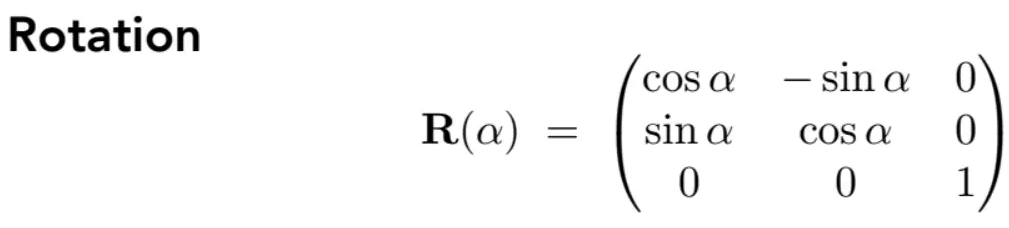
考虑如何分别绕三个坐标轴旋转,首先是绕x轴旋转:
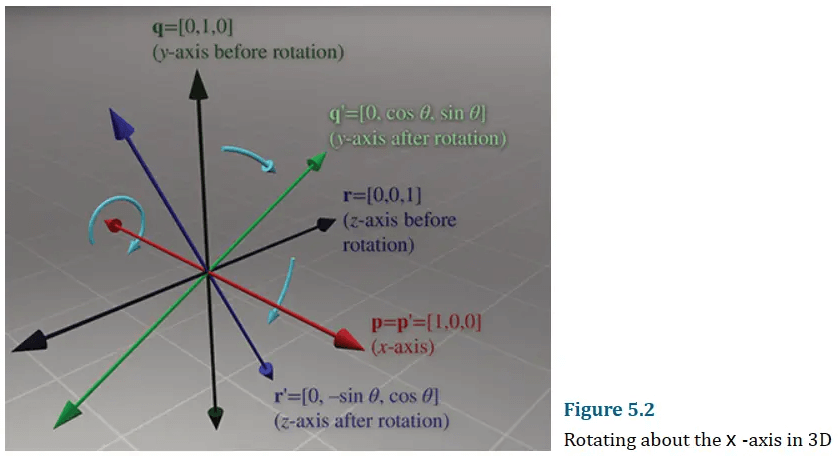
前面的文章说过,矩阵其实是向量的数组,因此我们可以用三个轴的方向向量来表示一个旋转矩阵。按照上图描述,基本旋转矩阵为:
Rx(θ)=∣p′∣∣q′∣∣r′∣=1000cosθsinθ0−sinθcosθ
用齐次坐标描述:
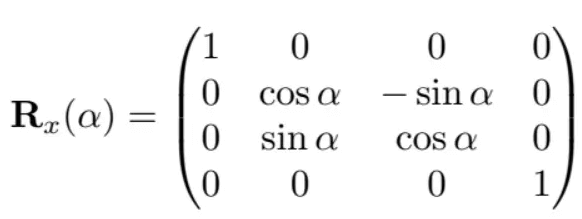
类似的,绕y轴旋转为:
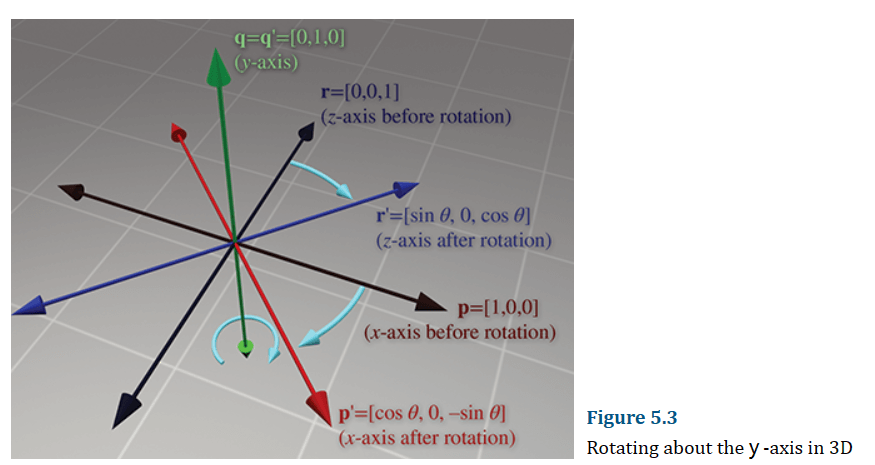
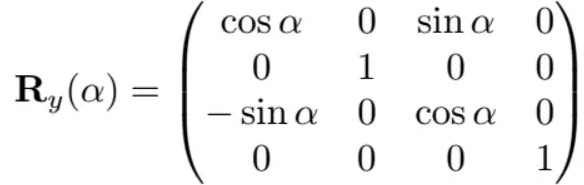
绕z轴旋转为:
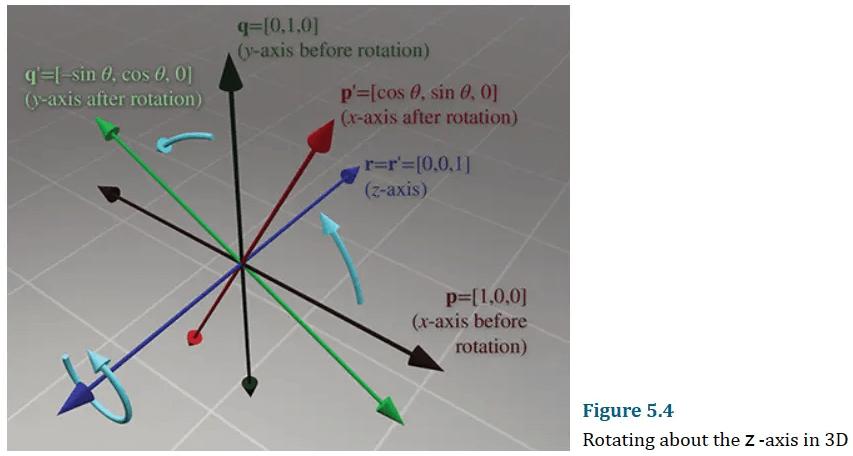
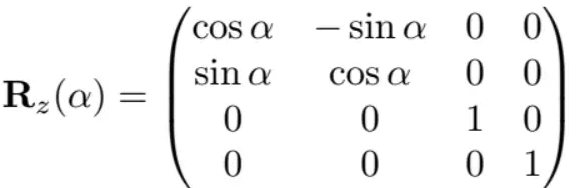
如果想要绕任意方向进行旋转,可以使用罗德里格斯旋转公式:

其中,n为旋转轴,用向量表示;α为旋转角度。默认旋转轴是过原点的,如果不过就先平移到原点旋转,再平移回去。
欧拉角
三维旋转也能通过使用欧拉角/四元数来表示,这里先看欧拉角。
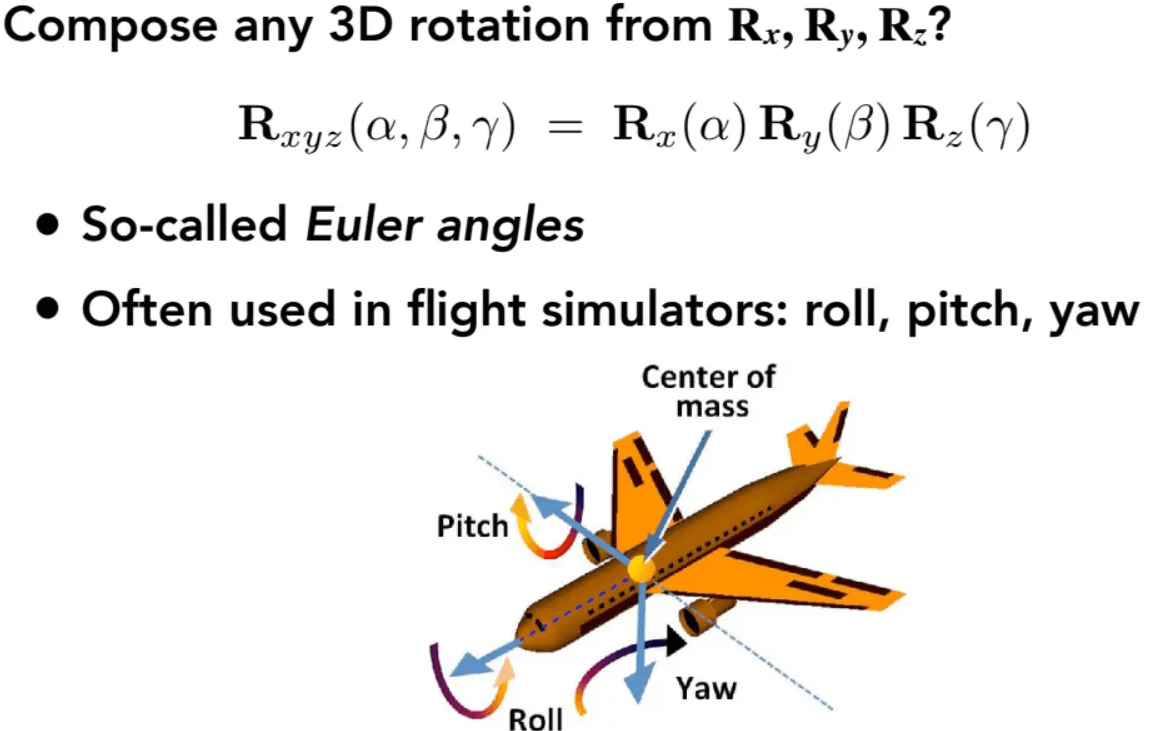
如上图所示,只需将3个绕轴旋转的矩阵结合起来就行了,这三个角在欧拉角中被称为偏航角(Yaw),翻滚角(Roll),俯仰角(Pitch)。
通常情况下,只会选择一个固定的顺序进行旋转,而这会导致**万向锁(Gimbal Lock)**发生。例如以ZYX顺序进行旋转,首先绕z旋转θz,然后绕y旋转90°,最后绕x旋转θx,也就是
Rzyx(θz, π/2, θx)=Rx(θx)Ry(π/2)Rz(θz)=0sin(θx+θz)−cos(θx+θz)0cos(θx+θz)sin(θx+θz)100=Ry(π/2)Rz(θx+θz)
可以发现此时旋转只由θx+θz决定,而不是三个旋转角,丢失了一个旋转自由度。
万向锁没有简单的解决方案,如果在使用欧拉角的过程中发生了万向锁,那么它们之间的插值可能会变得很怪异或摇摆不定,也就是产生“抖动”。
四元数
有关四元数的基础知识在这里。
定义相关元素如下:
- p=[0,v]表示3D中的一个点
- q=[cos(θ/2),sin(θ/2)n^],其中θ是要旋转的角度,n^是单位矢量旋转轴。这是通过轴-角系统的视角从而定义成这样的。
那么,p绕n^旋转θ°后的p′可由以下乘法运算得出:
p′=qpq−1
当然,旋转是可以叠加的,例如将p先旋转a,再旋转b,那么就相当于直接将p旋转ba:
p′=b(apa−1)b−1=(ba)p(a−1b−1)=(ba)p(ba)−1
仿射变换(Affine)
线性变换+平移变换。
平移变换(Translation)
矩阵形式如下:
[x′y′]=[1001][xy]+[txty]
显然,这种变换写不成线性变换的形式,因为它后边还有加法。我们不想让平移变换成为特例,于是引入齐次坐标,这样,平移就能写成”线性变换“的形式:
x′y′w′=100010txty1xy1=x+txy+ty1
这样,就能方便进行组合变换运算了。
引入齐次坐标系:
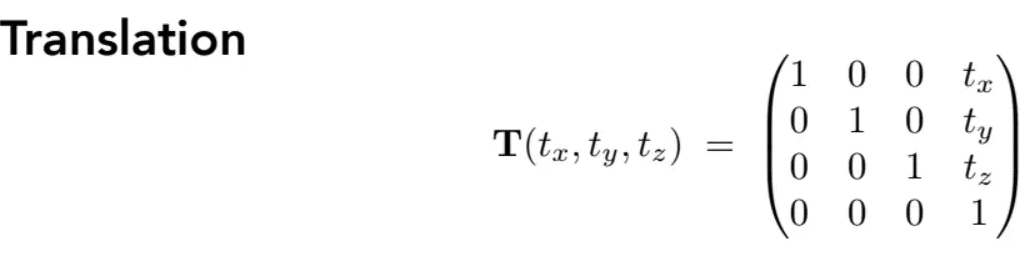
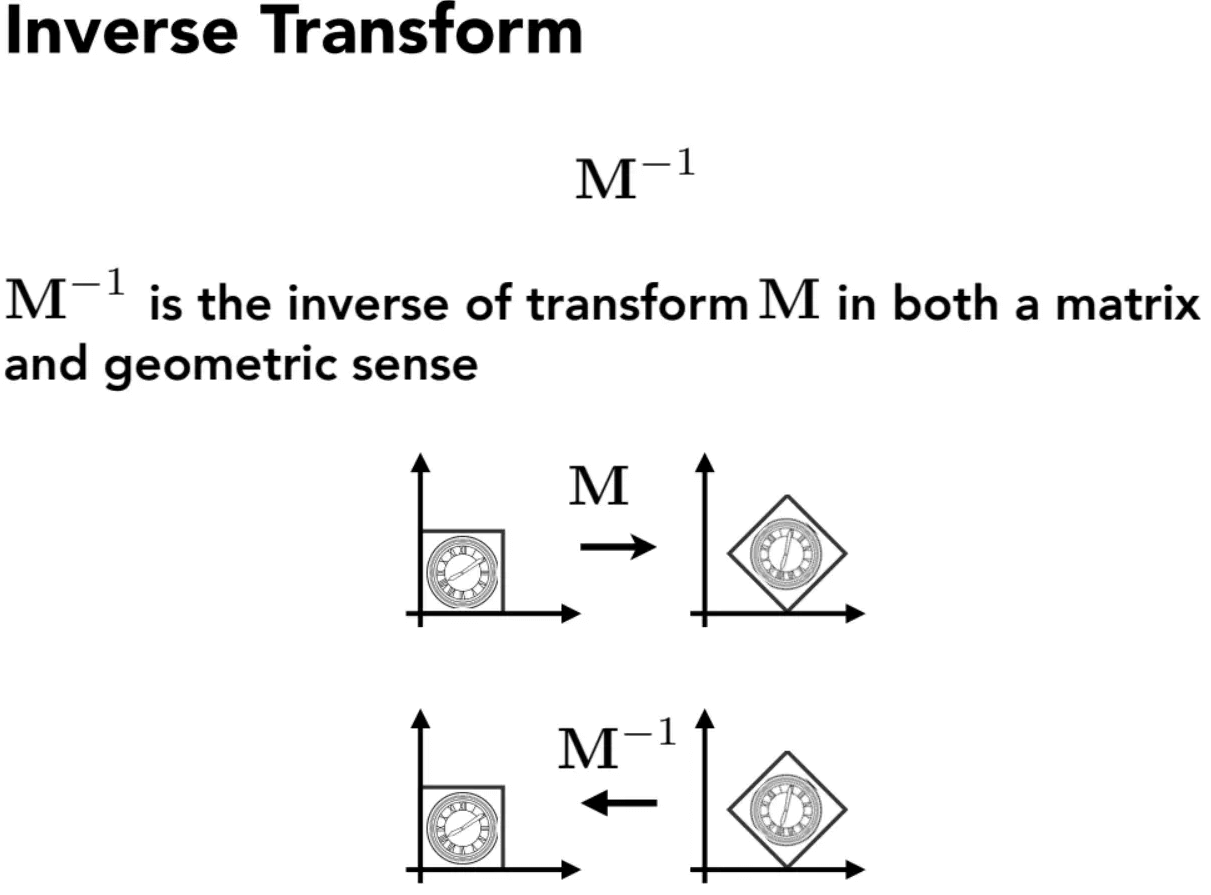
可逆变换(Invertible)
除了投影之外的所有原始变换都是可逆的。
组合变换
顾名思义,就是将上边一堆原始变换组合起来。
例如:
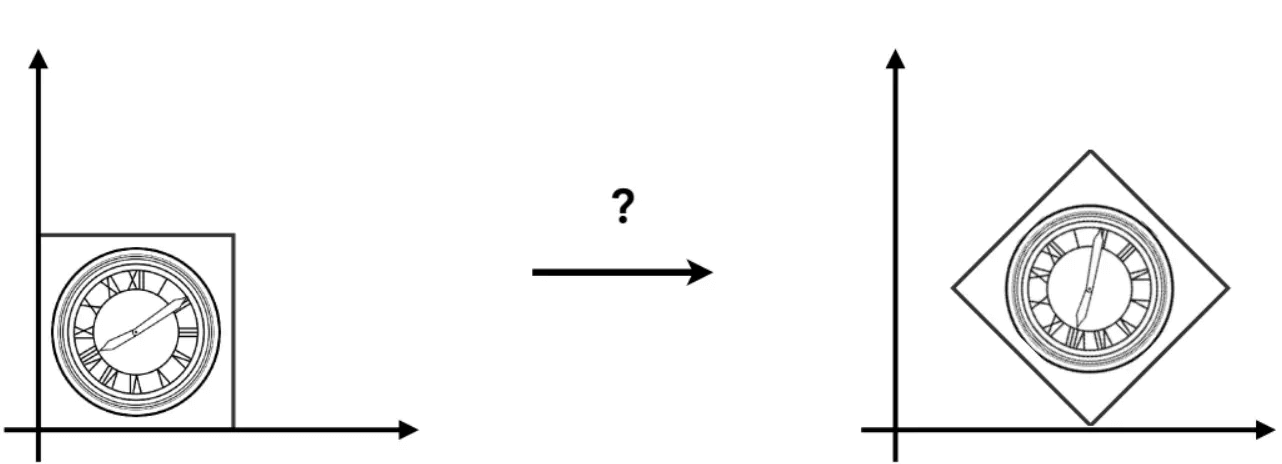
可以先绕原点旋转45°,然后平移过去 (注意变换的次序是重要的,颠倒过来再组合可能不是同一种变换了):
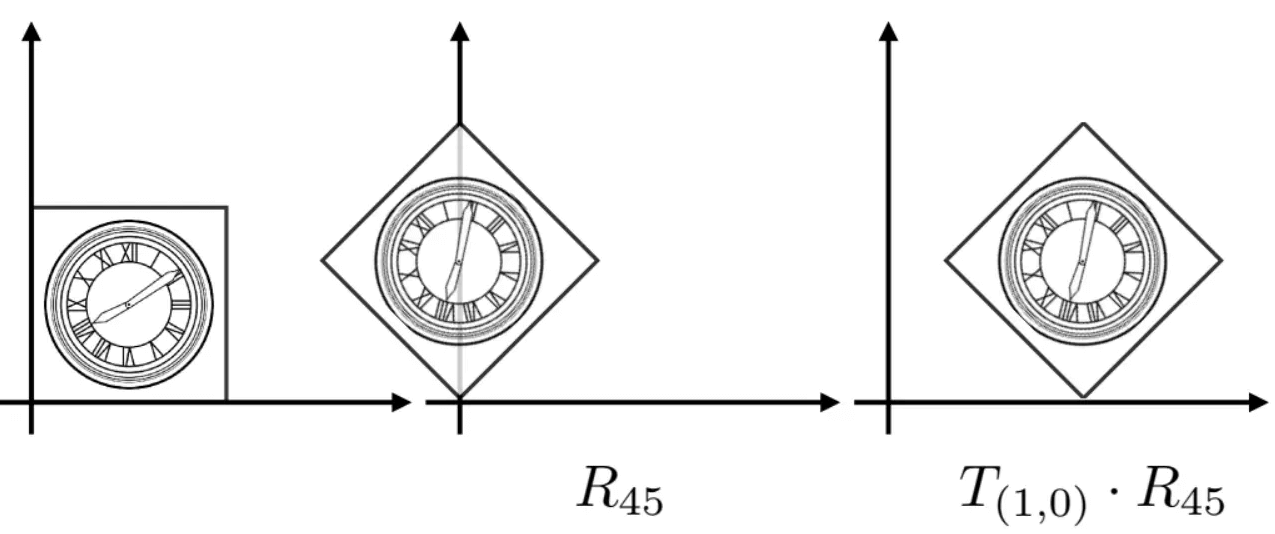
并且注意到,用列向量描述的前提下,矩阵是从右往左乘的:

为了计算简便,可以提前把这些变换矩阵给乘到一起。
参考资料