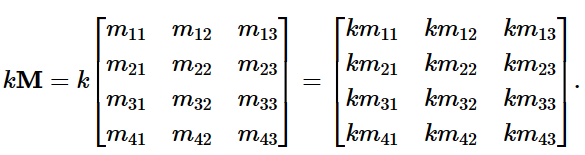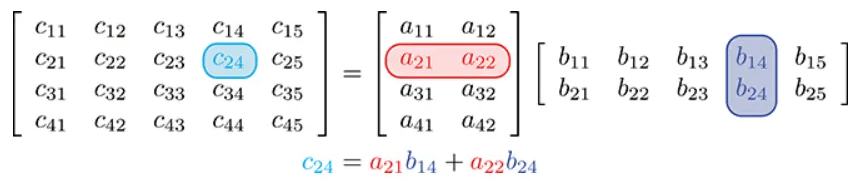03 - 矩阵(Matrix)

矩阵(Matrix)

向量是标量的数组，而矩阵是向量的数组。

单位矩阵(Identity Matrix)

维度为n的单位矩阵，表示为$\mathbf{I_n}$，是$n\times n$矩阵，其对角线上的值为1，其他元素均为0。三维的单位矩阵如下：

$$\nonumber \mathbf{I_3}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$$

矩阵转置(Transpose)

给定$r\times c$矩阵$\mathbf{M}$，其转置表示为$\mathbf{M^T}$，是$c\times r$矩阵，其中，列由$\mathbf{M}$的行构成。

例如：

$$\nonumber \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}^\mathbf{T} =\begin{bmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \\ \end{bmatrix}$$

一些结论：

• $(\mathbf{M^T})^\mathbf{T}=\mathbf{M}$
• $\mathbf{(AB)^T=B^T A^T}$

矩阵乘法

矩阵与标量相乘

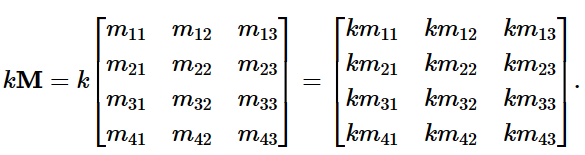
两个矩阵相乘

两个可以相乘的矩阵$\mathbf{AB}$，必须保证$\mathbf{A}$中的列数和$\mathbf{B}$中的行数相同，否则结果将是未定义的：

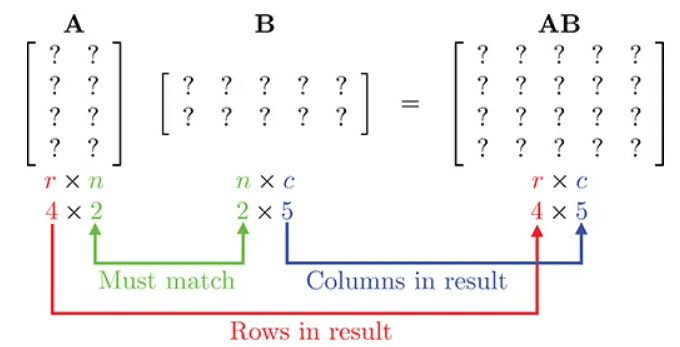
设$\mathbf{C=AB}$，则$\mathbf{C}$中的每一个元素$c_{ij}$等于$\mathbf{A}$的行i与$\mathbf{B}$的列j的向量点积：

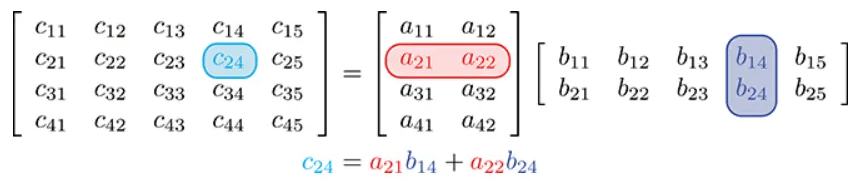
矩阵行列式(Determinant)

方形矩阵$\mathbf{M}$的行列式表示为$|\mathbf{M}|$，也可以表示为$\rm{det\ \mathbf{M}}$。

2x2和3x3行列式

例如，一个2x2行列式如下：

$$\nonumber |\mathbf{M}|= \begin{vmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{vmatrix}= m_{11}m_{22}-m_{12}m_{21}$$

一个3x3行列式如下：

$$\nonumber |\mathbf{M}|= \begin{vmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{vmatrix}= \begin{matrix} m_{11}(m_{22}m_{33}-m_{23}m_{32})\\ +\ m_{12}(m_{23}m_{31}-m_{21}m_{33})\\ +\ m_{13}(m_{21}m_{32}-m_{22}m_{31}) \end{matrix}$$

如果将3x3行列式看成3个行向量，那么该行列式就是3个行向量的三重积/混合积：

$$\nonumber \begin{vmatrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z} \end{vmatrix}= \begin{matrix} c_{x}(a_{y}b_{z}-a_{z}b_{y})\\ +c_{y}(a_{z}b_{x}-a_{x}b_{z})\\ +c_{z}(a_{x}b_{y}-a_{y}b_{x}) \end{matrix}= \mathbf{(a\times b)·c}$$

子矩阵行列式(Minor)和余子式(Cofactor)

假设$\mathbf{M}$是具有r行和c列的矩阵，删除它的i行和j列，得到一个r-1行和c-1列的新矩阵。如果子矩阵是行列式，可记为$M^{\{ij\}}$，被称为$\mathbf{M}$的子矩阵行列式。例如：

$$\nonumber \mathbf{M} = \begin{bmatrix} -4 & -3 & 3\\ 0 & 2 & -2\\ 1 & 4 & -1 \end{bmatrix} \Longrightarrow M^{\{12\}}= \begin{vmatrix} 0 & -2\\ 1 & -1 \end{vmatrix}=2$$

而余子式则是在子矩阵行列式的基础上带上了符号：

$$\nonumber C^{\{ij\}}=(-1)^{i+j}M^{\{ij\}}$$

n x n行列式

已知2x2和3x3行列式是怎么计算的，那么就能根据余子式递归地求解nxn行列式。首先，从矩阵中任选一行/列。然后，对于行/列中的每个元素，将此元素乘以相应的余子式，然后求和即可得出矩阵的行列式。

例如，任意选择行i，行列式可以这样计算：

$$\nonumber |\mathbf{M}|=\sum^n_{j=1}m_{ij}C^{\{ij\}}=\sum^n_{j=1}m_{ij}(-1)^{i+j}M^{\{ij\}}$$

以3x3矩阵为例：

$$\nonumber \begin{vmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{vmatrix}= m_{11} \begin{vmatrix} m_{22} & m_{23} \\ m_{32} & m_{33} \end{vmatrix} -m_{12} \begin{vmatrix} m_{21} & m_{23} \\ m_{31} & m_{33} \end{vmatrix} +m_{13} \begin{vmatrix} m_{21} & m_{22} \\ m_{31} & m_{32} \end{vmatrix}$$

一些特性

• 任何维度的单位矩阵的行列式为1
• $\mathbf{|AB|=|A||B|}$
• $\mathbf{|M^T|=|M|}$
• 如果矩阵某行/列都是0，则该矩阵行列式为0
• 交换任意行/列，会让行列式变负
• 将b行/列全部元素的k倍添加到a行/列，行列式值不会改变

逆矩阵(Inverse)

逆矩阵符合下式：

$$\nonumber \mathbf{M(M^{-1})=M^{-1}M=I}$$

注意，并非所有矩阵都有逆矩阵。

如果某矩阵具有逆矩阵，那么它是 可逆的(Invertible) 或 非奇异的(Nonsingular)；相反，没有逆矩阵的矩阵是不可逆或奇异的。

奇异矩阵的行列式为0。

伴随矩阵求逆

对于较大规模的矩阵求逆，可以通过高斯消元等方法实现；而对于2x2~4x4较小的矩阵，利用伴随矩阵求逆是比较简便的方法。其他方法详见：求逆矩阵的一些方法 - 知乎 (zhihu.com)

矩阵$\mathbf{M}$的经典伴随矩阵，表示为$\rm{adj}\ \mathbf{M}$，被定义为$\mathbf{M}$的余子式的矩阵的转置。

例如有个3x3矩阵，它的伴随矩阵如下：

$$\nonumber \operatorname{adj} \mathbf{M} = \begin{bmatrix} C^{\{11\}} & C^{\{12\}} & C^{\{13\}}\\ C^{\{21\}} & C^{\{22\}} & C^{\{23\}}\\ C^{\{31\}} & C^{\{32\}} & C^{\{33\}} \end{bmatrix}^{\mathsf{T}}$$

可以通过伴随矩阵和行列式求得逆矩阵：

$$\nonumber \mathbf{M}^{-1}=\frac{\rm{adj}\ \mathbf{M}}{|\mathbf{M}|}$$

一些特性

• $\mathbf{(M^{-1})^{-1}=M}$
• $\mathbf{I^{-1}=I}$
• $\mathbf{(M^{-1})^{T}=(M^{T})^{-1}}$
• $\mathbf{(AB)^{-1}=B^{-1}A^{-1}}$
• $\mathbf{|M^{-1}|=1/|M|}$

正交矩阵(Orthogonal Matrix)

定义

当且仅当矩阵及其转置的乘积是单位矩阵时，方形矩阵$\mathbf{M}$是正交的：

$$\nonumber \mathbf{M}\ \text{是正交矩阵} \Longleftrightarrow \mathbf{MM^T=I}$$

根据逆矩阵的定义，发现如下性质：

$$\nonumber \mathbf{M}\ \text{是正交矩阵} \Longleftrightarrow \mathbf{M^T=M^{-1}}$$

该性质常用于快速求正交矩阵的逆。

如何判断

要使矩阵正交，必须满足以下条件：

• 矩阵的每一行必须是单位矢量
• 矩阵的行必须相互垂直

可以对矩阵的列进行类似描述，因为如果矩阵正交，转置矩阵也正交。

正交化(Orthogonalize)

我们希望通过此操作得到一个矩阵，该矩阵具有相互垂直的单位矢量轴，并且尽可能地接近原矩阵。

（待补充，无偏差的递增正交化算法）

参考资料

• GAMES101-现代计算机图形学入门
• 3D数学基础 图形和游戏开发(第2版)