02 - PRT
能解决实时环境光照的除了IBL外,还有PRT(Precomputed Radiance Transfer)。本文将先介绍一些PRT的数学基础(信号、基函数、球谐函数等),然后介绍PRT的算法,最后介绍一点2D小波函数内容。
回顾数学基础
信号
首先简要回顾一下在GAMES101中有关信号的内容。
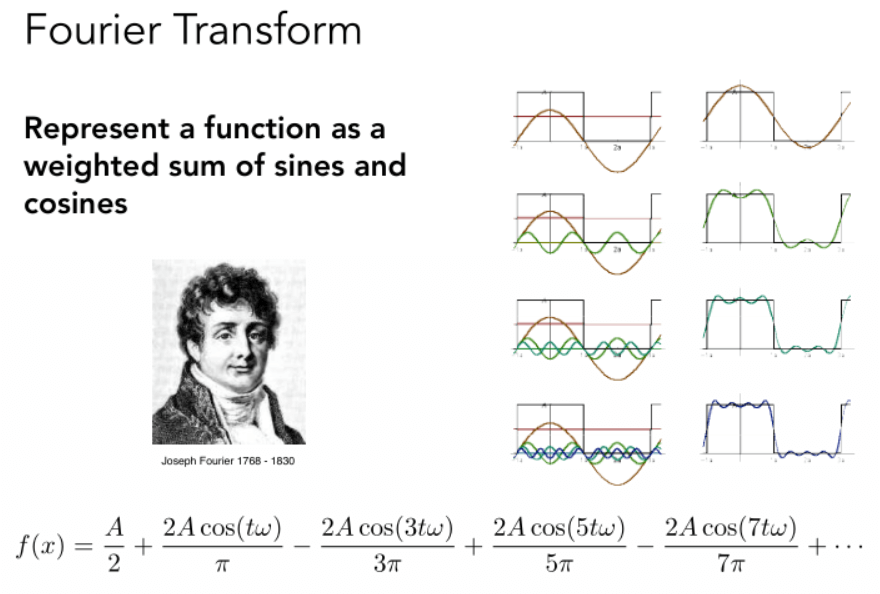
傅里叶变换
函数f(x)可由一个常数项和若干sin, cos项近似表示。并且每个项都有自己的频率。
图片的频率
图片可通过傅里叶变换将时域转换为频域,右图也被称为图片的频谱图:
因此,可用不同大小的滤波核对图像进行过滤操作,保留需要的信息。例如下图使用 低通滤波器(Low-pass filter),只保留图片的低频信息:
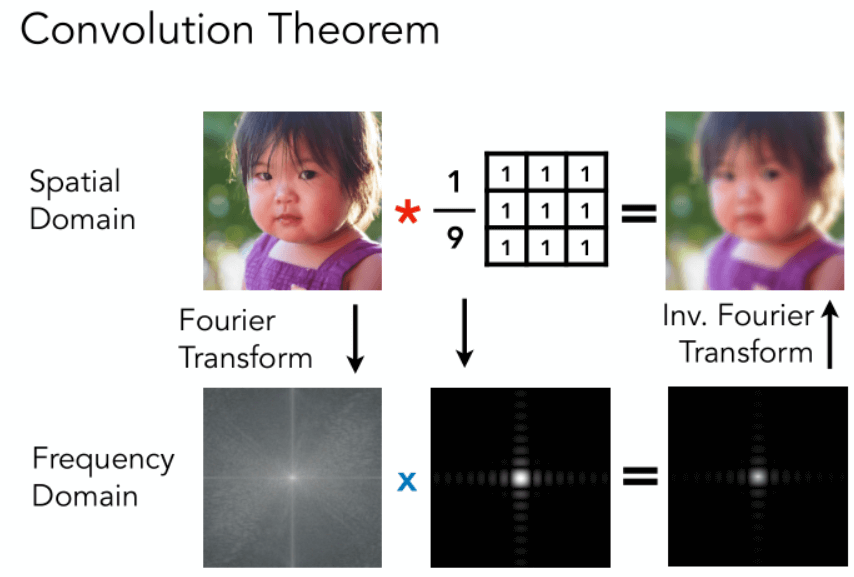
卷积理论
在时域的卷积操作相当于在频域的乘积操作:
一些公理
-
两个函数乘积的积分可悲认为是滤波/卷积操作:
-
认为低频率就是函数光滑/变化满等。
-
认为上面说的滤波操作中,它的最终频率是各函数中的最低频率。
基函数
函数f(x)可被很多其他函数的线性组合描述:
例如傅里叶展开系列,多项式系列都是基函数。
球谐函数(SH)
定义
球谐函数(Spherical Harmonics, SH),是一系列定义在球面上的二维基函数(用两个角描述球面坐标,因此是二维);也可看做是一维情况下的傅里叶函数。
它很适合用来直接分析球面上一些函数的性质。
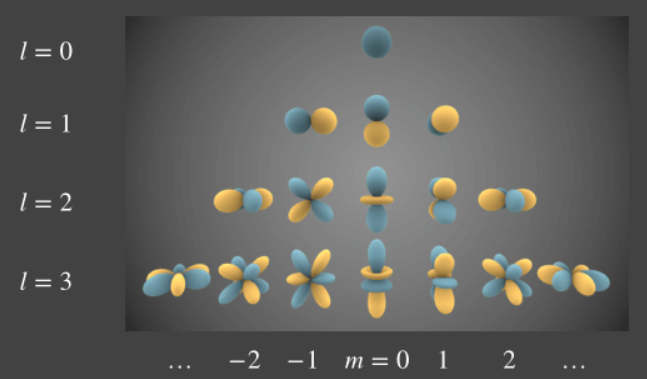
在这个图中:
- 每行SH的频率都相同;
- 颜色表示函数值的符号,值的大小是离原点的距离;
- SH的阶数l与球谐函数数量的关系:;
- m是每一阶SH的编号;
- 前n阶SH的总数为:。
性质
正交性
SH 是正交的,每个SH基函数都由一个勒让德(Legendre)多项式组成。
简单投影/重建
可通过**投影(Projection)**操作获得每个SH基函数前面的系数:
然后就能用若干项基函数和它前面的系数来 重建(Reconstruction) SH所描述的函数f(x)。引入SH的阶数越高,描述的高频信息也就相对越多。
简单旋转
旋转一个SH,相当于旋转它的正交基。因此旋转后的SH可被 同阶基函数SH 线性表示。
简单卷积
SH可进行简单的卷积操作。
低频
SH重建出来的原函数是低频的,保留不了多少高频信息。
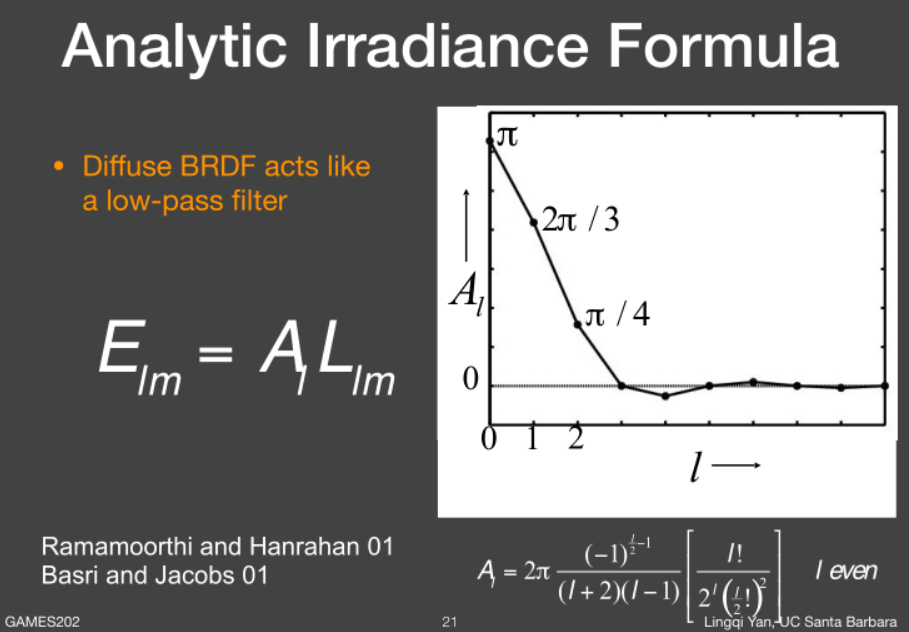
应用
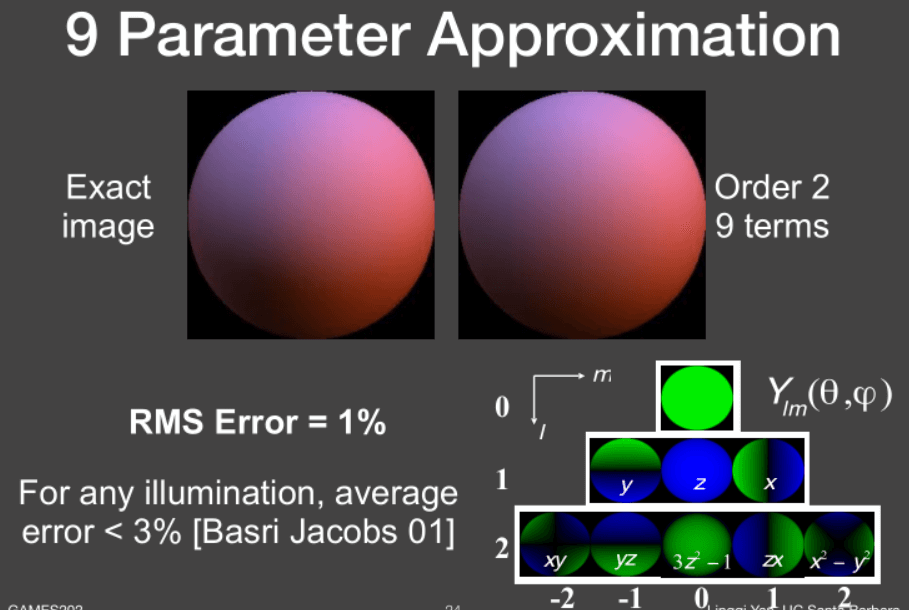
如图,diffuse BRDF可由前3阶的SH简要描述。从配图来看,diffuse BRDF是没有高频信息的,因为3阶以后的值基本为0。因此,diffuse BRDF是低频函数,而且光滑,就像一个低通滤波器。
而这样的低通滤波器和环境光照的映射(相当于一个球面函数)相乘,就相当于做了个滤波/卷积操作,就能完成下图的预过滤阶段:
经研究发现,应使用前3阶共9个SH去描述diffuse BRDF,误差只有1%:
对于任何光照条件,只要物体材质是diffuse的,就都能用前三阶SH描述。
有了以上数学基础,就能开始PRT内容了。
PRT
使用IBL进行环境光照的着色很好,但难解决阴影问题。而 PRT(Precomputed Radiance Transfer) 则不必担心阴影问题,它是 考虑阴影的环境光照,也是 静态场景的全局光照。
背景
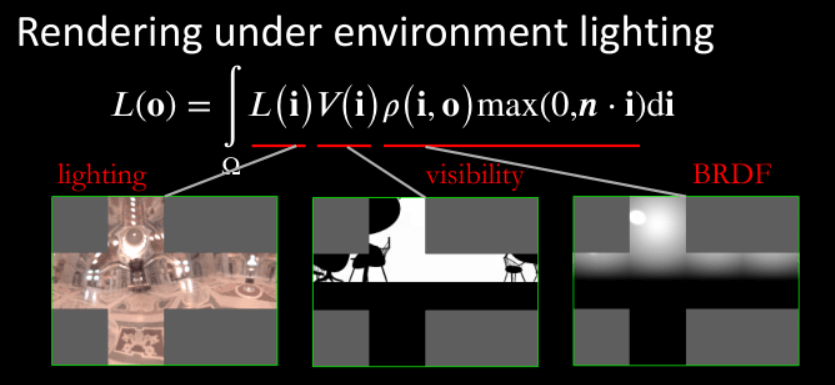
回顾一下考虑阴影(可见性)的RTR渲染方程:
其中,环境光,可见性,BRDF均可被存储为球面贴图。
如果使用暴力法求解渲染方程,那么需要对三个贴图进行采样,然后计算乘积。假设每张图小正方形的分辨率为64x64,那渲染一个着色点需要3x6x64x64次采样,很慢。
我们能不能像IBL那样,简化渲染方程从而简化计算呢?这正是PRT所做的事。
算法
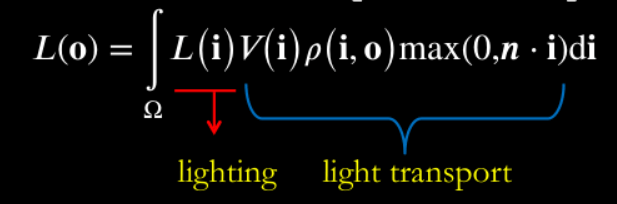
如图,PRT认为 整个场景只有光照在改变,可将渲染方程分为两部分:光照(Lighting) 和 光传输(Lighting Transport) 两部分。
PRT将光照项用基函数近似表示;而光传输部分是不变的,也能用基函数近似表示,可对它进行预计算,然后投影到基函数空间中。
在运行时只需通过几个乘法便完成了渲染方程的运算,很快。
diffuse材质
如果材质是diffuse的,那么BRDF就是个常数,将它提取出来:
然后我们用基函数近似光照项:
带入渲染方程,有
我们发现,这个积分项就是可进行预计算的光传输项在某基函数SH上的投影。
因此有
现在只需计算向量点乘即可完成渲染方程的计算,如何计算点乘?下图给出答案:
glossy材质
如果材质是glossy的,那么BRDF就不是常数,是,一个四维函数。那么有:
发现右边有个2D函数,计算复杂。
接下来将用基函数(SH)近似:
那么就有:
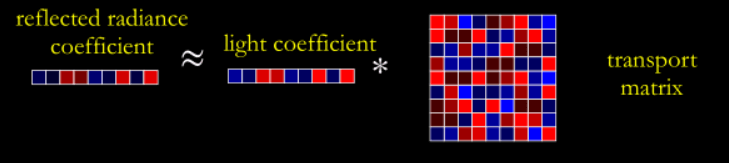
将这些项可视化表示,就是:
- Shading结果,关于的一维向量;
- ,一维向量;
- ,二维矩阵。
我们只需计算向量和矩阵的乘积就能解出渲染方程。
代价
但代价是什么?
- 空间上:任何一个着色点都要存储这个transport矩阵
- 时间上:通常选用3/4/5阶SH描述,导致
diffuse情况需要次点乘;glossy情况需要次向量矩阵乘法。
多次弹射
前面只说了环境光弹射一次的情况,这里讨论一下环境光弹射多次的情况(它们都差不多)。
描述光传输路径
我们可以像编译原理那样描述光的传输路径:
LE:直接光照,反射光直接进入眼睛,对应下图none情况。LGE:反射光会弹到glossy材质物体上,然后再次反射进入眼睛,对应下图 1 bounce 情况。L(D|G)*E:LGE的通用版本。反射光会弹到diffuse/glossy材质物体上,并且会再次经反射弹到diffuse/glossy物体上......直到弹射*次后才反射进入眼睛,对应下图 2 bounces 情况。LS*(D|G)*E:在前者基础上,光线会先到specular材质物体上进行多次反弹,然后才会做前者的工作,对应下图 caustics 情况。
因此,任何光路可被描述为 L + Transport,而后者可被预计算,不影响运行时时间。
对光传输的理解
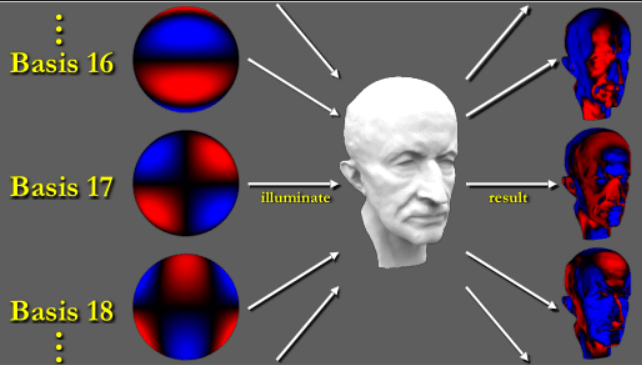
如图,光传输的计算可理解为,求在不同SH基函数下计算渲染方程(着色),然后将着色结果综合起来。
总结
PRT使用SH近似描述了渲染方程的光照项和光传输项,我们在预计算阶段计算并存储光传输的所有可能结果,然后在运行时,将光照项和光传输项进行点乘/向量矩阵乘法即可(方式取决于物体的材质)。
当然,PRT也存在一些限制:
- 由于使用球谐函数SH作为基函数,它只能描述低频的内容,不适合描述高频的(因为付出代价很大,往往要26阶才能描述较准确)
- 虽然光源可以是动态的,但场景、材质必须是静态的。因为后者是经过预计算的。
- 预计算需要的数据存储太大。
为了缓解这些限制,人们也是做了许多工作:
- 使用更多种类的基函数;
- 让两个积分点乘变成三个;
- 允许场景、材质稍微动态一点;
- 将PRT应用在更多领域(半透明材质,头发等);
- 通过推导解析解进而减少预计算。
更多基函数
除了球谐函数SH,多项式函数等基函数外,还有很多:
- 小波函数(Wavelet)
- 带球调和函数(Zonal Harmonics)
- 球面高斯函数(Spherical Gaussian,SG)
- 阶跃长函数(Piecewise Constant)
小波函数
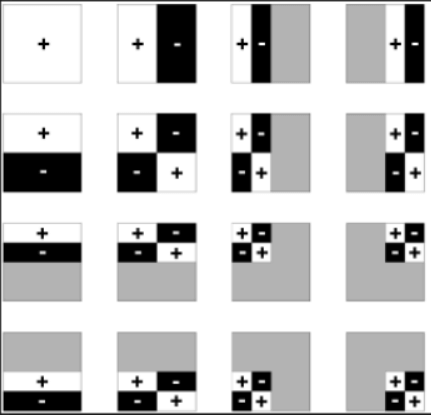
这里介绍的是2D Haar小波函数,它定义在图像块上。
特点
-
投影操作:
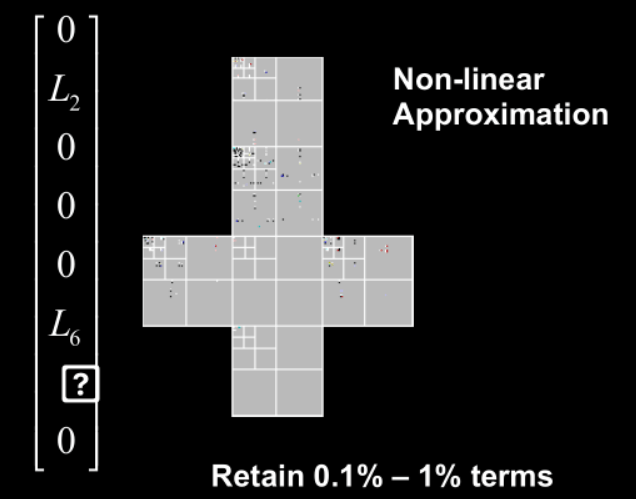
可以将图像投影到各个基函数上,然后保留系数不为0的项,进而得到近似结果。这种近似也被称为非线性(non-linear)近似。
-
支持全频率:
小波函数的特性支持它描述全频率的信息。
应用
可以对CubeMap上的每个图做小波变换,高频信息留在左下,右下,右上三块;低频信息放在左上。然后左上又能做一次小波变换……
渲染结果如下,可见很好地描述了高频信息: